16 Inference for a single proportion
Focusing now on statistical inference for categorical data, we will revisit many of the foundational aspects of hypothesis testing from Chapter 11.
The three data structures we detail are one binary variable, summarized using a single proportion; two binary variables, summarized using a difference of two proportions; and two categorical variables, summarized using a two-way table. When appropriate, each of the data structures will be analyzed using the three methods from Chapter 11, Chapter 12, and Chapter 13: randomization test, bootstrapping, and mathematical models, respectively.
As we build on the inferential ideas, we will visit new foundational concepts in statistical inference. For example, we will cover the conditions for when a normal model is appropriate; the two different error rates in hypothesis testing; and choosing the confidence level for a confidence interval.
We encountered inference methods for a single proportion in Chapter 12, exploring point estimates and confidence intervals. In this section, we’ll do a review of these topics and how to choose an appropriate sample size when collecting data for single proportion contexts.
Note that there is only one variable being measured in a study which focuses on one proportion. For each observational unit, the single variable is measured as either a success or failure (e.g., “surgical complication” vs. “no surgical complication”). Because the nature of the research question at hand focuses on only a single variable, there is not a way to randomize the variable across a different (explanatory) variable. For this reason, we will not use randomization as an analysis tool when focusing on a single proportion. Instead, we will apply bootstrapping techniques to test a given hypothesis, and we will also revisit the associated mathematical models.
16.1 Bootstrap test for a proportion
The bootstrap simulation concept when
We expand on the medical consultant example from Section 12.1, but instead of finding an interval estimate for the true complication rate, we test a specific claim.
16.1.1 Observed data
Recall the set-up for the example: People providing an organ for donation sometimes seek the help of a special “medical consultant”. These consultants assist the patient in all aspects of the surgery, with the goal of reducing the possibility of complications during the medical procedure and recovery. Patients might choose a consultant based in part on the historical complication rate of the consultant’s clients. One consultant tried to attract patients by noting the average complication rate for liver donor surgeries in the US is about 10%, but her clients have only had 3 complications in the 62 liver donor surgeries she has facilitated. She claims this is strong evidence that her work meaningfully contributes to reducing complications (and therefore she should be hired!).
Using the data, is it possible to assess the consultant’s claim that her complication rate is less than 10%?
No. The claim is that there is a causal connection, but the data are observational. Patients who hire this medical consultant may have lower complication rates for other reasons.
While it is not possible to assess this causal claim, it is still possible to test for an association using these data. For this question we ask, could the low complication rate of
Write out hypotheses in both plain and statistical language to test for the association between the consultant’s work and the true complication rate,
Because, as it turns out, the conditions of working with the normal distribution are not met (see Section 16.2), the uncertainty associated with the sample proportion should not be modeled using the normal distribution, as doing so would underestimate the uncertainty associated with the sample statistic. However, we would still like to assess the hypotheses from the previous Guided Practice in absence of the normal framework. To do so, we need to evaluate the possibility of a sample value
The p-value is computed based on the null distribution, which is the distribution of the test statistic if the null hypothesis is true. Supposing the null hypothesis is true, we can compute the p-value by identifying the probability of observing a test statistic that favors the alternative hypothesis at least as strongly as the observed test statistic. Here we will use a bootstrap simulation to calculate the p-value.
16.1.2 Variability of the statistic
We want to identify the sampling distribution of the test statistic
Under the null hypothesis, 10% of liver donors have complications during or after surgery. Suppose this rate was really no different for the consultant’s clients (for all the consultant’s clients, not just the 62 previously measured). If this was the case, we could simulate 62 clients to get a sample proportion for the complication rate from the null distribution. Simulating observations using a hypothesized null parameter value is often called a parametric bootstrap simulation, but we will refer to it descriptively as “simulating under the null hypothesis claim.”
Similar to the process described in Chapter 12, each client can be simulated using a bag of marbles with 10% red marbles and 90% white marbles. Sampling a marble from the bag (with 10% red marbles) is one way of simulating whether a patient has a complication if the true complication rate is 10%. If we select 62 marbles and then compute the proportion of patients with complications in the simulation,
There were 5 simulated cases with a complication and 57 simulated cases without a complication, i.e.,
Is this one simulation enough to determine whether we should reject the null hypothesis?
No. To assess the hypotheses, we need to see a distribution of many values of
16.1.3 Observed statistic vs. null statistics
One simulation isn’t enough to get a sense of the null distribution; many simulation studies are needed. Roughly 10,000 seems sufficient. However, paying someone to simulate 10,000 studies by hand is a waste of time and money. Instead, simulations are typically programmed into a computer, which is much more efficient.
Figure 16.1 shows the results of 10,000 simulated studies. The proportions that are equal to or less than
Of the 10,000 simulated
Because the estimated p-value is 0.117, which is larger than the discernibility level 0.05, we cannot reject the null hypothesis. Explain what this means in plain language in the context of the problem.2
Does the conclusion in the previous Guided Practice imply the consultant is good at their job? Explain.3
Null distribution of
Regardless of the statistical method chosen, the p-value is always derived by analyzing the null distribution of the test statistic. The normal model poorly approximates the null distribution for
In the previous Guided Practice, the p-value is estimated. It is not exact because the simulated null distribution itself is only a close approximation of the sampling distribution of the sample statistic. An exact p-value can be generated using the binomial distribution, but that method will not be covered in this text.
16.2 Mathematical model for a proportion
16.2.1 Conditions
In Section 13.2, we introduced the normal distribution and showed how it can be used as a mathematical model to describe the variability of a statistic. There are conditions under which a sample proportion
Sampling distribution of
The sampling distribution for
- The sample’s observations are independent, e.g., are from a simple random sample.
- We expected to see at least 10 successes and 10 failures in the sample, i.e.,
When these conditions are met, then the sampling distribution of
Recall that the margin of error is defined by the standard error. The margin of error for
Margin of error for
The margin of error is
Typically we do not know the true proportion
The independence condition is a more nuanced requirement. When it isn’t met, it is important to understand how and why it is violated. For example, there exist no statistical methods available to truly correct the inherent biases of data from a convenience sample. On the other hand, if we took a cluster sample (see Section 2.1.5), the observations wouldn’t be independent, but suitable statistical methods are available for analyzing the data (but they are beyond the scope of even most second or third courses in statistics).
In the examples based on large sample theory, we modeled
The independence assumption may be reasonable if each of the surgeries is from a different surgical team. However, the success-failure condition is not satisfied. Under the null hypothesis, we would anticipate seeing
While this book is scoped to well-constrained statistical problems, do remember that this is just the first book in what is a large library of statistical methods that are suitable for a very wide range of data and contexts.
16.2.2 Confidence interval for a proportion
A confidence interval provides a range of plausible values for the parameter
Standard error of one proportion,
When the conditions are met so that the distribution of
Note that we almost never know the true value of
For hypothesis testing, we use
Consider taking many polls of registered voters (i.e., random samples) of size 300 asking them if they support legalized marijuana. It is suspected that about 2/3 of all voters support legalized marijuana. To understand how the sample proportion
16.2.3 Variability of the sample proportion
A simple random sample of 826 payday loan borrowers was surveyed to better understand their interests around regulation and costs. 70% of the responses supported new regulations on payday lenders.
Is it reasonable to model the distribution of
Estimate the standard error of
Construct a 95% confidence interval for
- The data are a random sample, so it is reasonable to assume that the observations are independent and representative of the population of interest. We also must check the success-failure condition, using
- Using
Constructing a confidence interval for a single proportion.
There are three steps to constructing a confidence interval for
- Check if it seems reasonable to assume the observations are independent and check the success-failure condition using
- Calculate the standard error using
- Apply the general confidence interval formula.
For additional one-proportion confidence interval examples, see Section 12.3.
16.2.4 Changing the confidence level
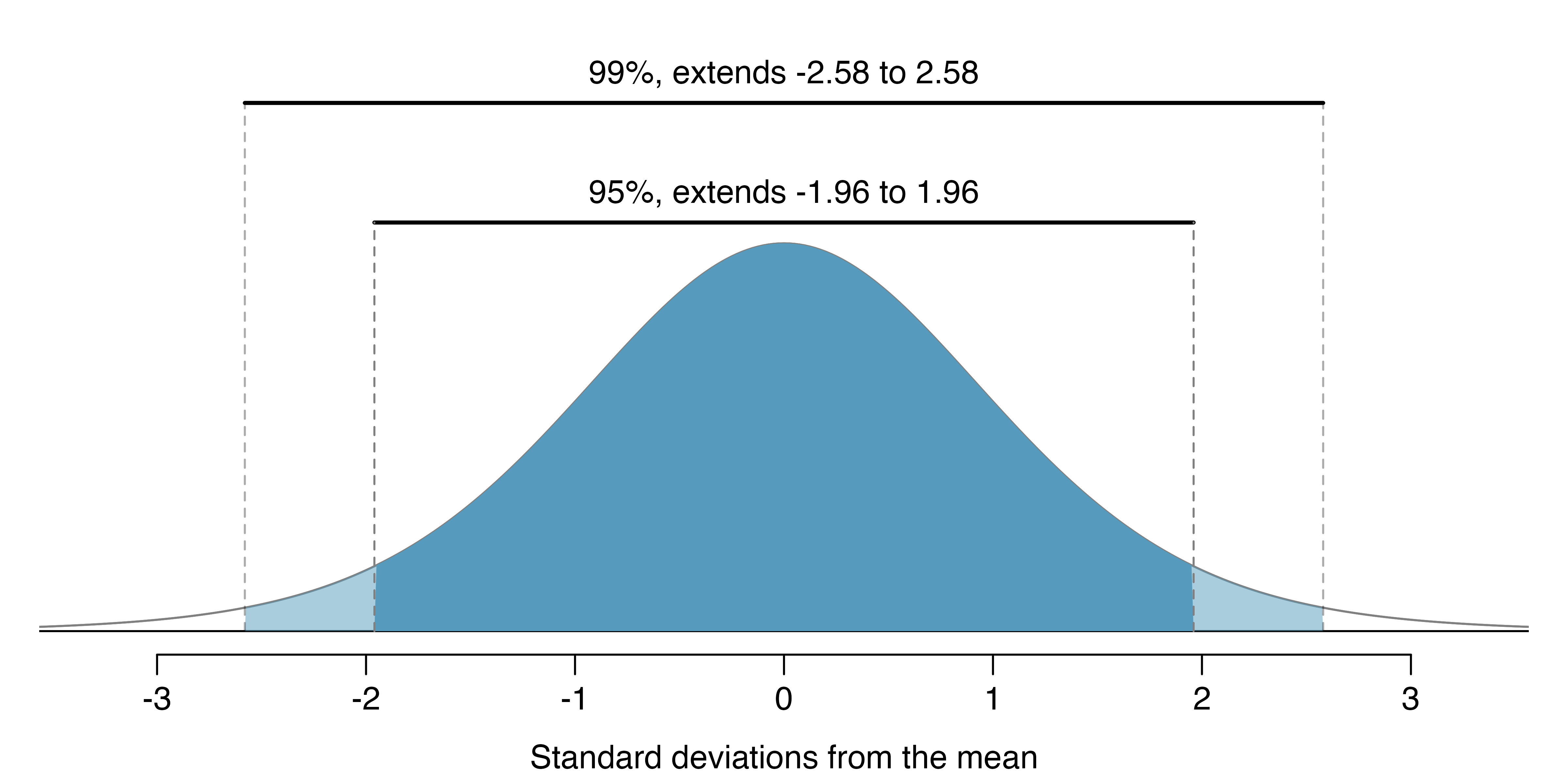
Suppose we want to consider confidence intervals where the confidence level is somewhat higher than 95%: perhaps we would like a confidence level of 99%. Think back to the analogy about trying to catch a fish: if we want to be more sure that we will catch the fish, we should use a wider net. To create a 99% confidence level, we must also widen our 95% interval. On the other hand, if we want an interval with lower confidence, such as 90%, we could make our original 95% interval slightly slimmer.
The 95% confidence interval structure provides guidance in how to make intervals with new confidence levels. Below is a general 95% confidence interval for a point estimate that comes from a nearly normal distribution:
There are three components to this interval: the point estimate, “1.96”, and the standard error. The choice of
If
To create a 99% confidence interval, change 1.96 in the 95% confidence interval formula to be
The normal approximation is crucial to the precision of the
Create a 99% confidence interval for the impact of the stent on the risk of stroke using the data from Section 1.1. The point estimate is 0.090, and the standard error is
Mathematical model confidence interval for any confidence level.
If the point estimate follows the normal model with standard error
where
Figure 16.2 provides a picture of how to identify
Previously, we found that implanting a stent in the brain of a patient at risk for a stroke increased the risk of a stroke. The study estimated a 9% increase in the number of patients who had a stroke, and the standard error of this estimate was about
16.2.5 Hypothesis test for a proportion
One possible regulation for payday lenders is that they would be required to do a credit check and evaluate debt payments against the borrower’s finances. We would like to know: would borrowers support this form of regulation?
Set up hypotheses to evaluate whether borrowers have a majority support for this type of regulation.8
To apply the normal distribution framework in the context of a hypothesis test for a proportion, the independence and success-failure conditions must be satisfied. In a hypothesis test, the success-failure condition is checked using the null proportion: we verify
The test statistic for assessing a single proportion is a Z.
The Z score is a ratio of how the sample proportion differs from the hypothesized proportion
When the null hypothesis is true and the conditions are met, Z has a standard normal distribution.
Conditions:
- independent observations
- large samples
Do payday loan borrowers support a regulation that would require lenders to pull their credit report and evaluate their debt payments? From a random sample of 826 borrowers, 51% said they would support such a regulation. Is it reasonable to use a normal distribution to model
Mathematical model hypothesis test for a proportion.
Set up hypotheses and verify the conditions using the null value,
For additional one-proportion hypothesis test examples, see Section 11.3.
Using the hypotheses and data from the previous Guided Practices, evaluate whether the poll on lending regulations provides convincing evidence that a majority of payday loan borrowers support a new regulation that would require lenders to pull credit reports and evaluate debt payments.
With hypotheses already set up and conditions checked, we can move onto calculations. The standard error in the context of a one-proportion hypothesis test is computed using the null value,
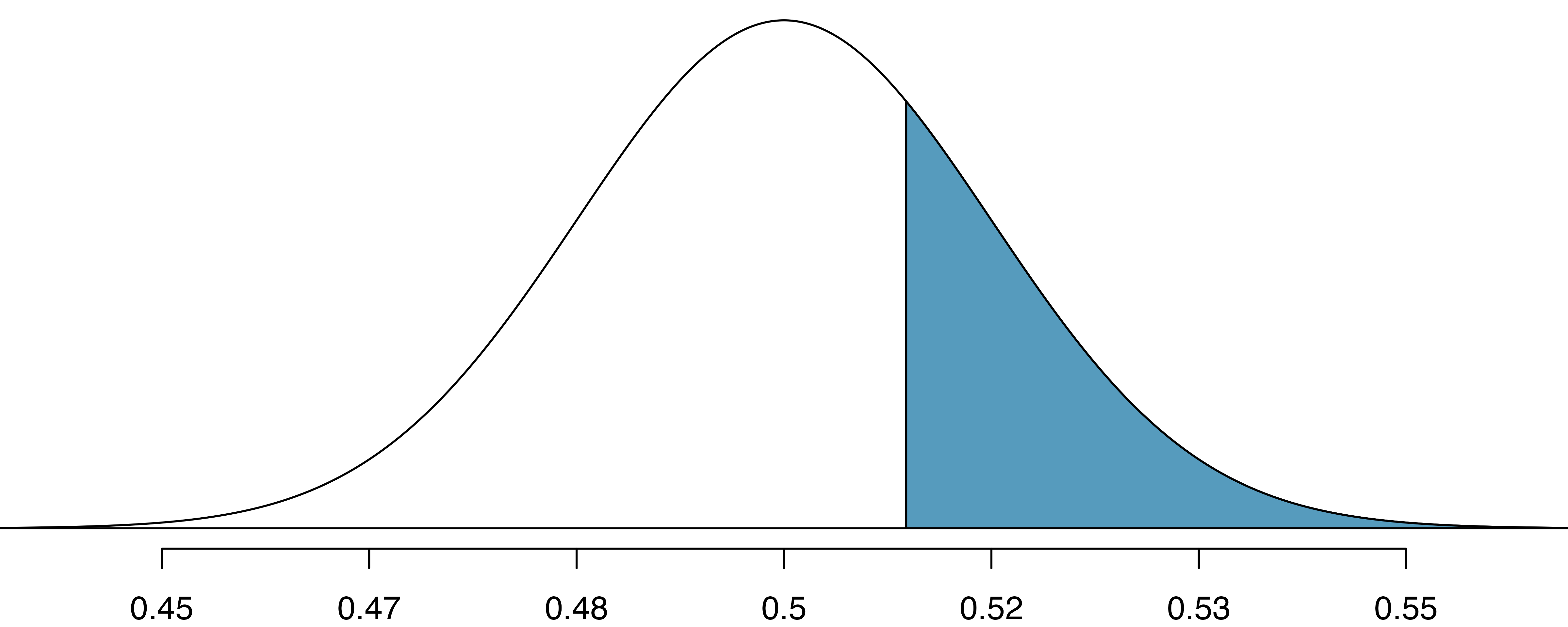
A picture of the normal model is shown below with the p-value represented by the shaded region.
Based on the normal model, the test statistic can be computed as the Z score of the point estimate:
The single tail area which represents the p-value is 0.2776. Because the p-value is larger than 0.05, we do not reject
In Section 17.1 we discuss two-sided hypothesis tests of which the payday example may have been better structured. That is, we might have wanted to ask whether the borrowers support or oppose the regulations (to study opinion in either direction away from the 50% benchmark). In that case, the p-value would have been doubled to 0.5552 (again, we would not reject
In both the one-sided or two-sided setting, the conclusion is somewhat unsatisfactory because there is no conclusion. That is, there is no resolution one way or the other about public opinion. We cannot claim that exactly 50% of people support the regulation, but we cannot claim a majority in either direction.
16.2.6 Violating conditions
We’ve spent a lot of time discussing conditions for when
When the success-failure condition isn’t met for a hypothesis test, we can simulate the null distribution of
16.3 Chapter review
16.3.1 Summary
Building on the foundational ideas from the previous few ideas, this chapter focused exclusively on the single population proportion as the parameter of interest. Note that it is not possible to do a randomization test with only one variable, so to do computational hypothesis testing, we applied a bootstrapping framework. The bootstrap confidence interval and the mathematical framework for both hypothesis testing and confidence intervals are similar to those applied to other data structures and parameters. When using the mathematical model, keep in mind the success-failure conditions. Additionally, know that bootstrapping is always more accurate with larger samples.
16.3.2 Terms
The terms introduced in this chapter are presented in Table 16.1. If you’re not sure what some of these terms mean, we recommend you go back in the text and review their definitions. You should be able to easily spot them as bolded text.
16.4 Exercises
Answers to odd-numbered exercises can be found in Appendix A.16.
-
Do aliens exist? In May 2021, YouGov asked 4,839 adult Great Britain residents whether they think aliens exist, and if so, if they have or have not visited Earth. You want to evaluate if more than a quarter (25%) of Great Britain adults think aliens don’t exist. In the survey 22% responded “I think they exist, and have visited Earth”, 28% responded “I think they exist, but have not visited Earth”, 29% responded “I don’t think they exist”, and 22% responded “Don’t know”. A friend of yours offers to help you with setting up the hypothesis test and comes up with the following hypotheses. Indicate any errors you see.
-
Married at 25. A study suggests that the 25% of 25 year-olds have gotten married. You believe that this is incorrect and decide to collect your own sample for a hypothesis test. From a random sample of 776 25 year-olds, you find that 24% of them are married. A friend of yours offers to help you with setting up the hypothesis test and comes up with the following hypotheses. Indicate any errors you see.
-
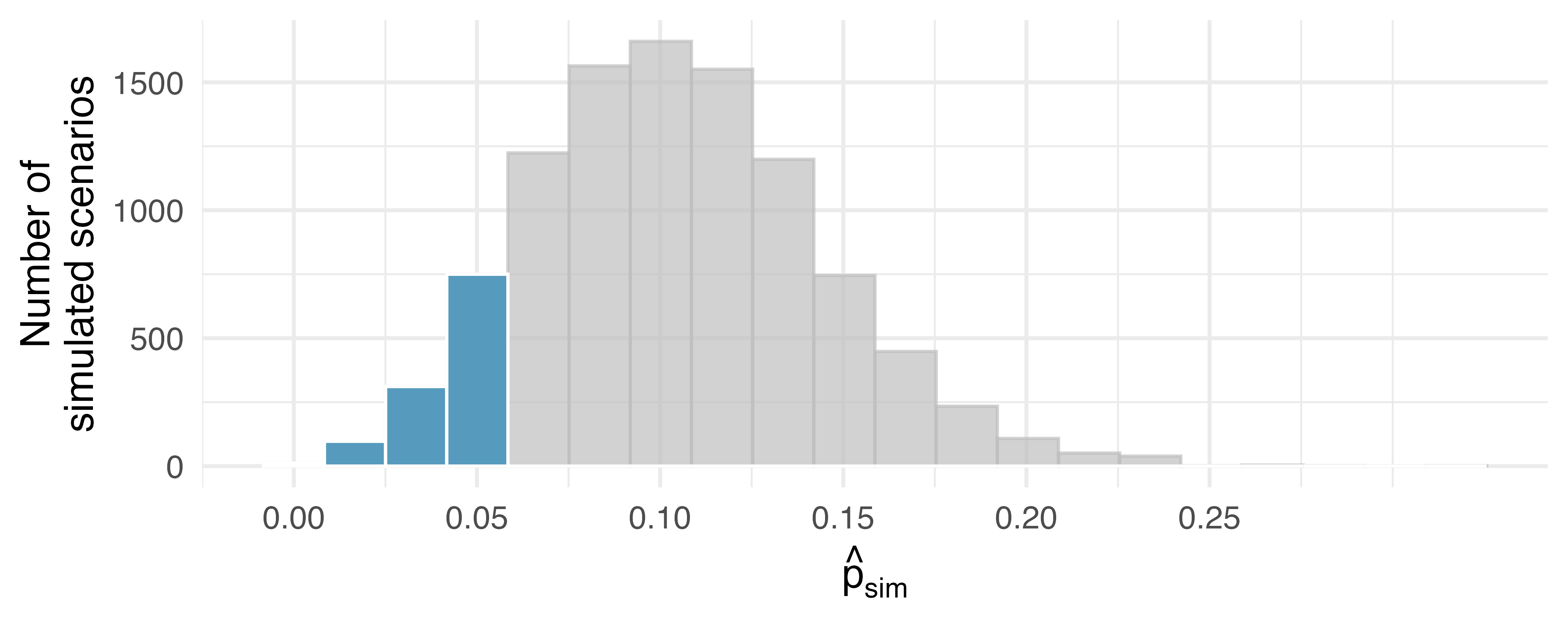
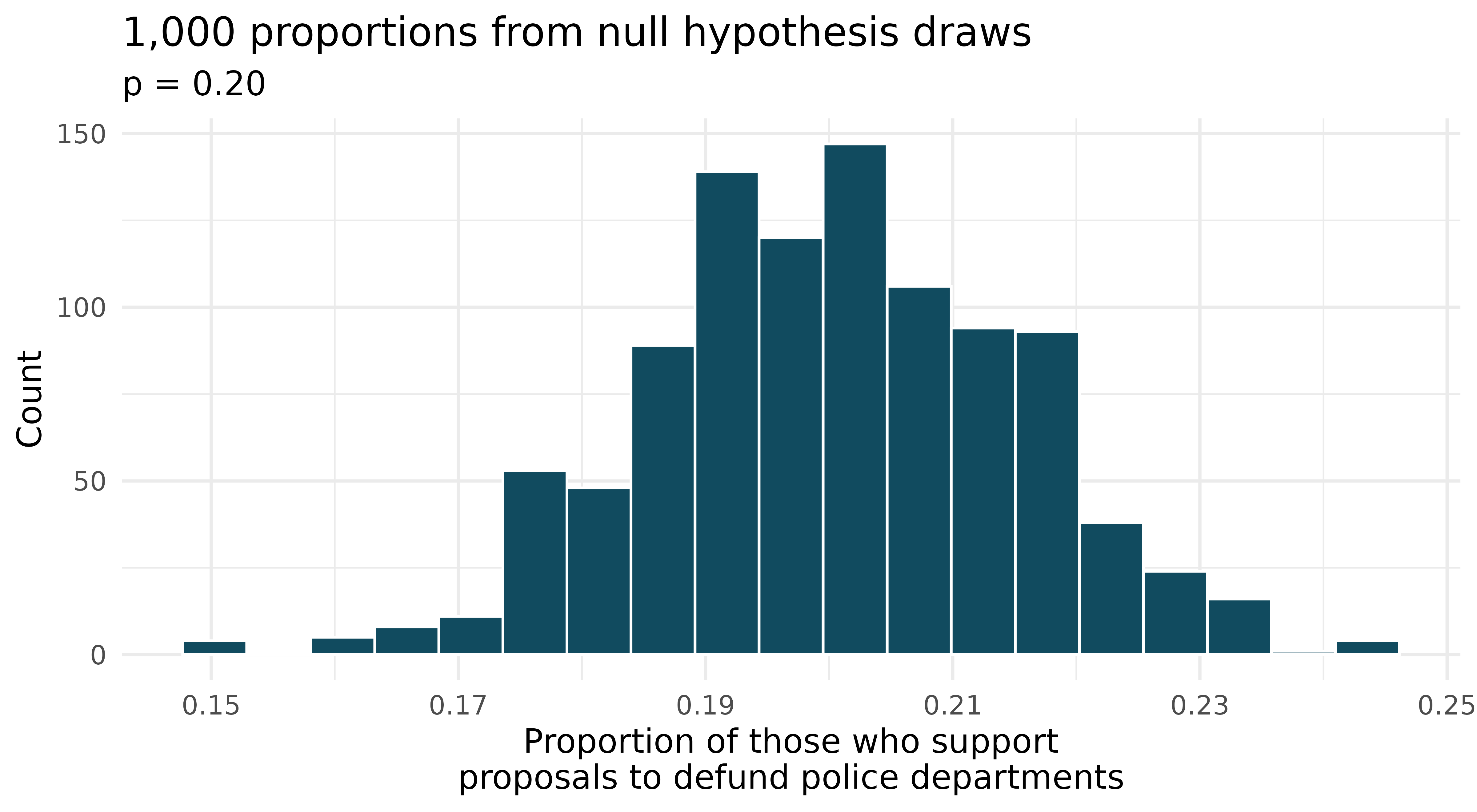
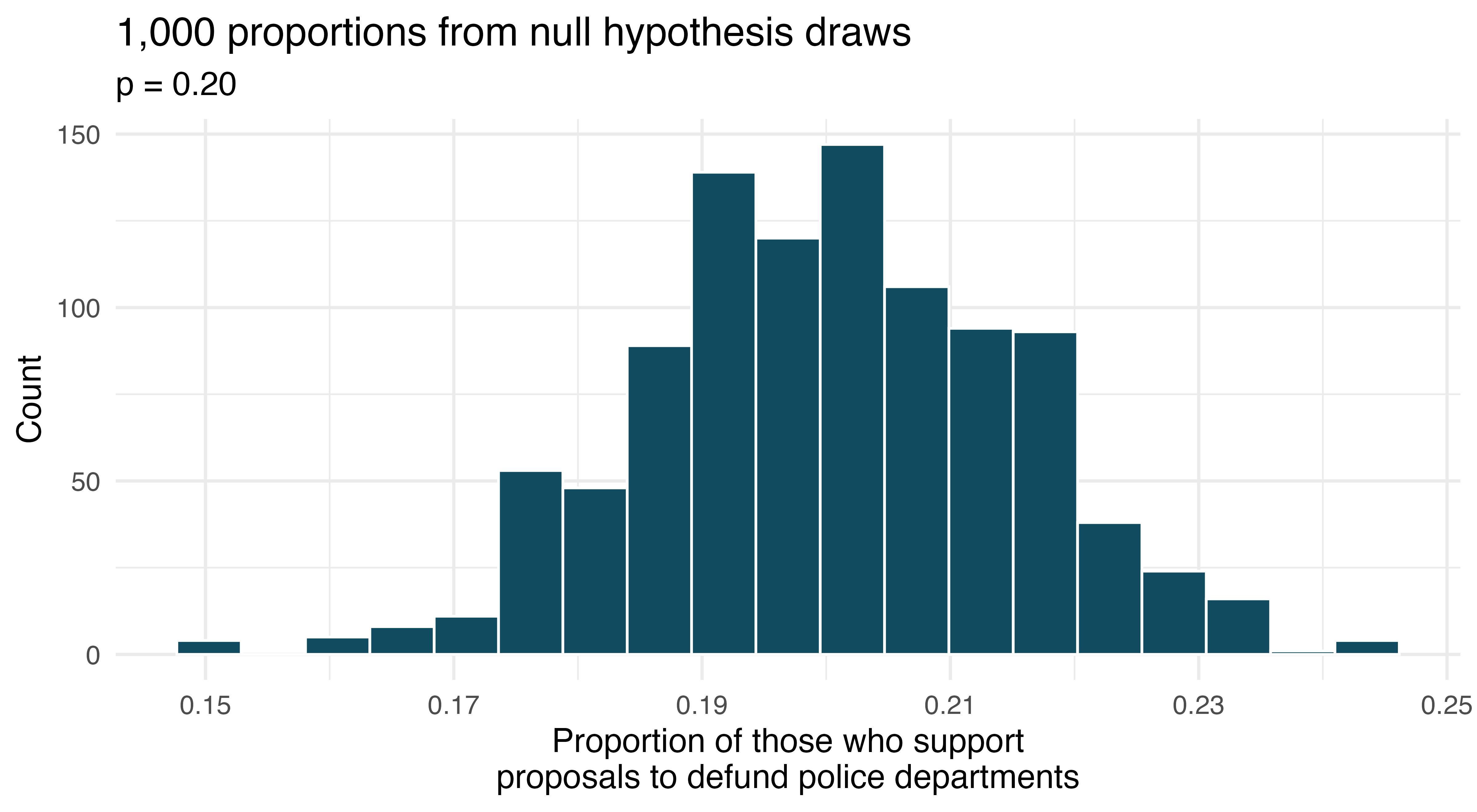
Defund the police. A Survey USA poll conducted in Seattle, WA in May 2021 reports that of the 650 respondents (adults living in this area), 159 support proposals to defund police departments. (Survey USA 2021)
A journalist writing a news story on the poll results wants to use the headline “More than 1 in 5 adults living in Seattle support proposals to defund police departments.” You caution the journalist that they should first conduct a hypothesis test to see if the poll data provide convincing evidence for this claim Write the hypotheses for this test.
Calculate the proportion of Seattle adults in the sample who support proposals to defund police departments.
Describe a setup for a simulation that would be appropriate in this situation and how the p-value can be calculated using the simulation results.
The histogram below shows the distribution of 1,000
-
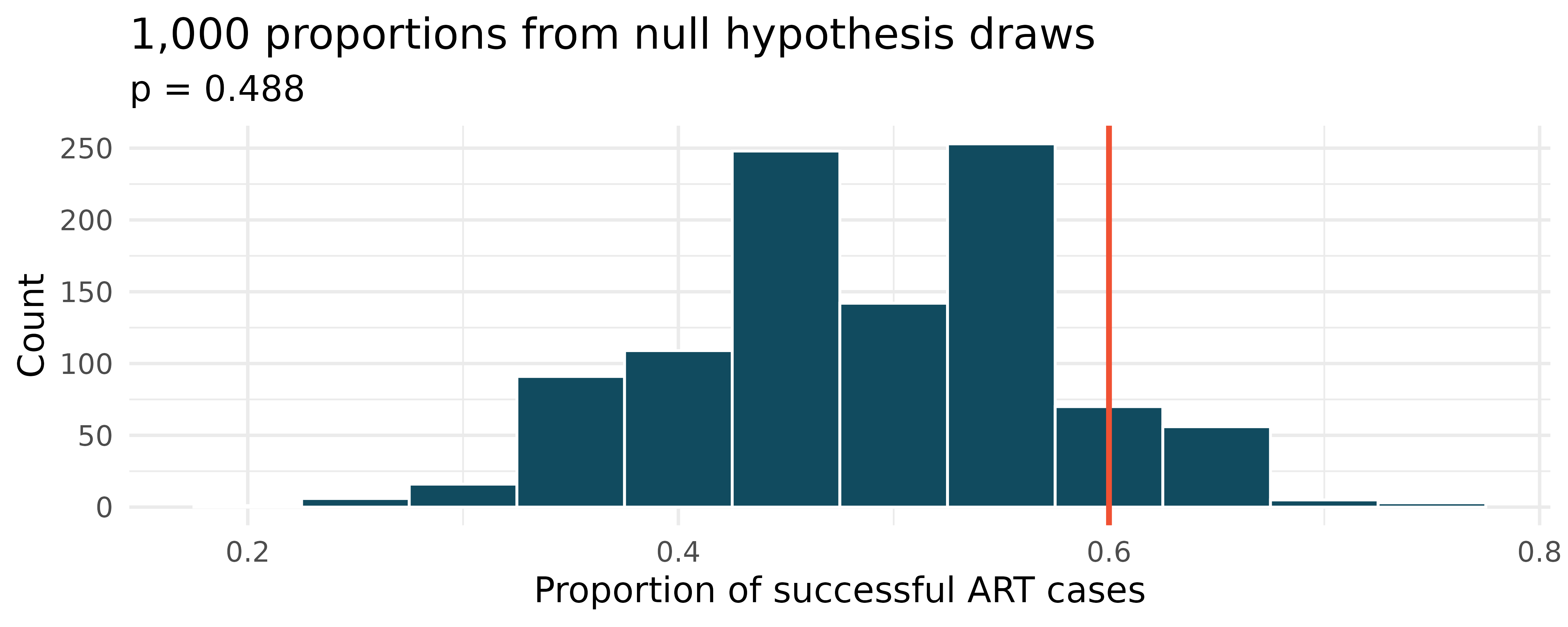
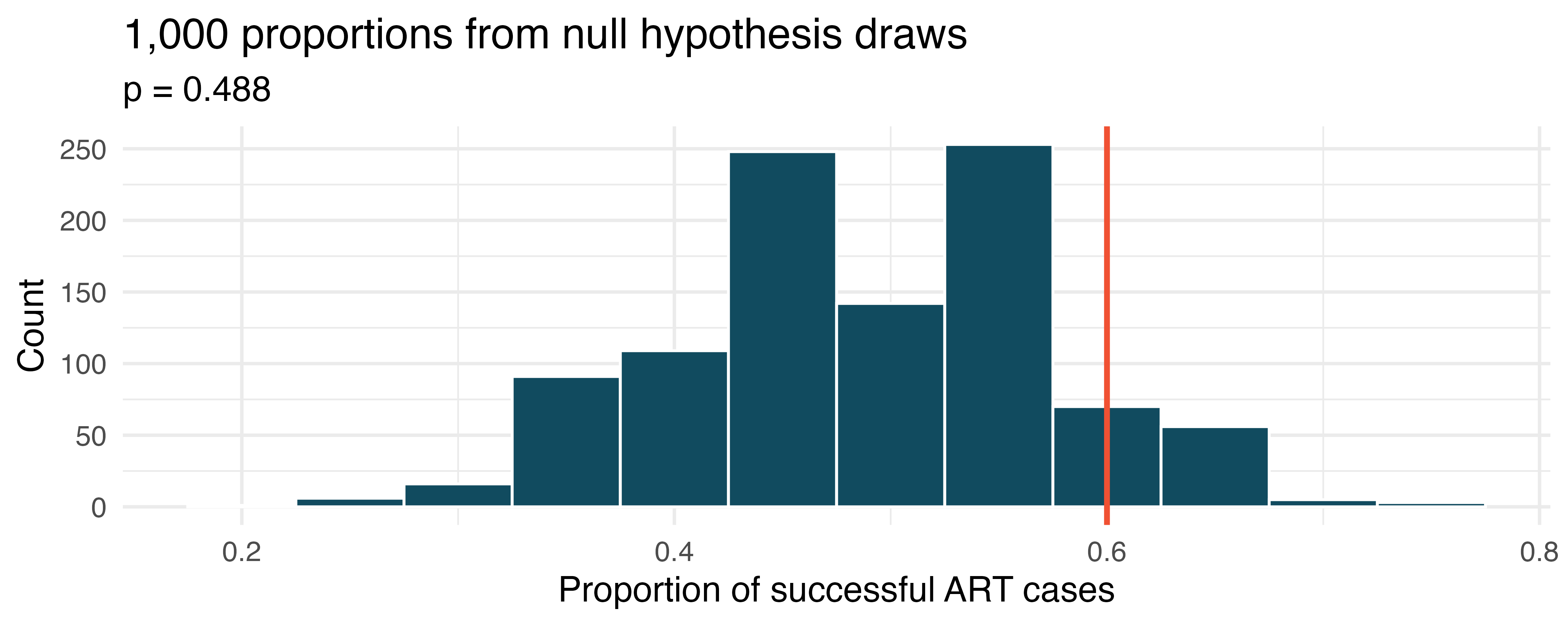
Assisted reproduction. Assisted Reproductive Technology (ART) is a collection of techniques that help facilitate pregnancy (e.g., in vitro fertilization). The 2018 ART Fertility Clinic Success Rates Report published by the Centers for Disease Control and Prevention reports that ART has been successful in leading to a live birth in 48.8% of cases where the patient is under 35 years old. (CDC 2018) A new fertility clinic claims that their success rate is higher than average for this age group. A random sample of 30 of their patients yielded a success rate of 60%. A consumer watchdog group would like to determine if the data provides strong evidence to support the company’s claim.
Write the hypotheses to test if the success rate for ART at this clinic is discernibly higher than the success rate reported by the CDC.
Describe a setup for a simulation that would be appropriate in this situation and how the p-value can be calculated using the simulation results.
The histogram below shows the distribution of 1,000
- After performing this analysis, the consumer group releases the following news headline: “Infertility clinic falsely advertises better success rates”. Comment on the appropriateness of this statement.
-
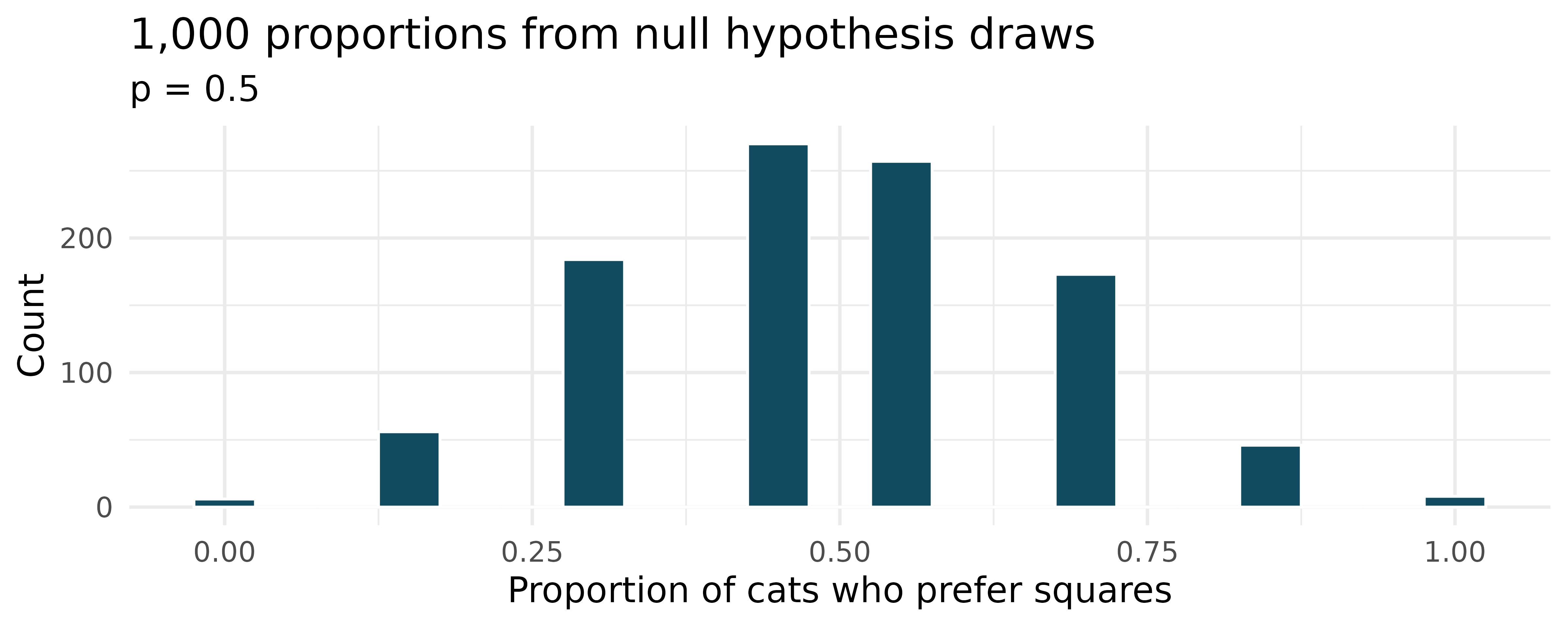
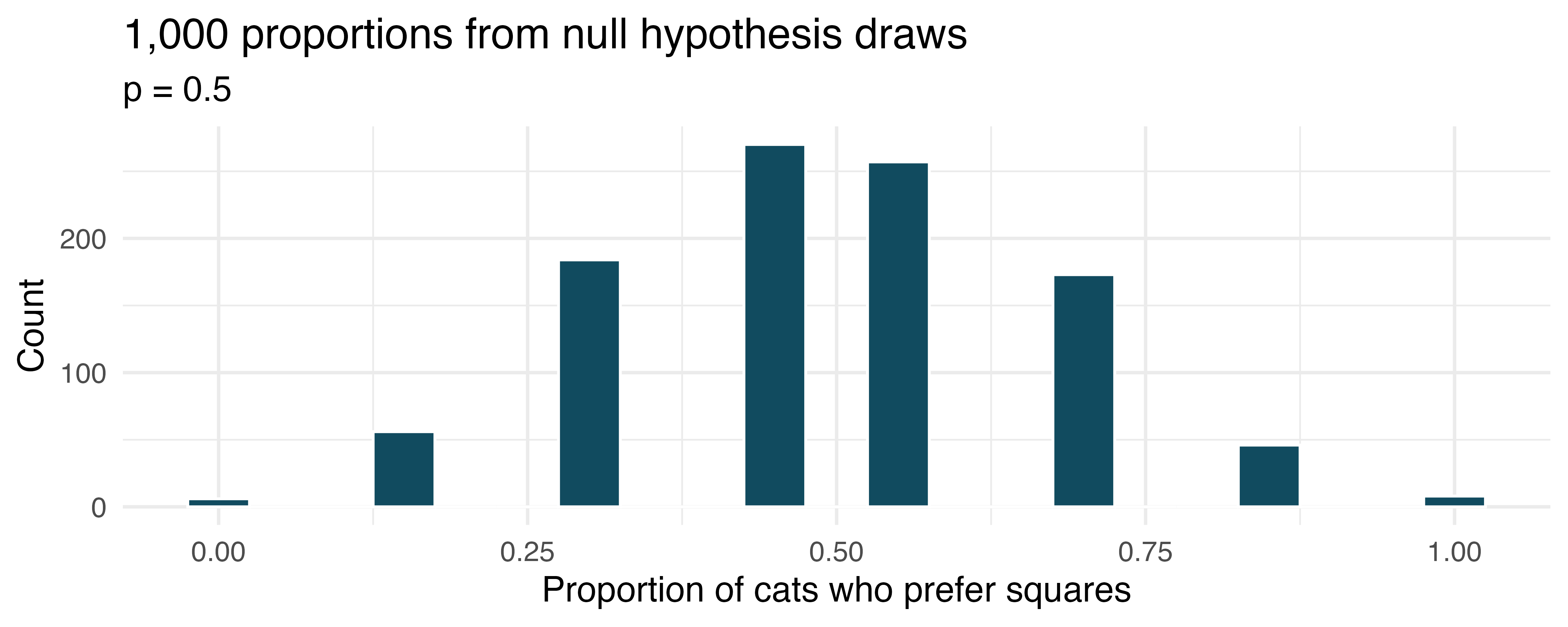
If I fits, I sits, simulated null hypothesis. A citizen science project on which type of enclosed spaces cats are most likely to sit in compared (among other options) two different spaces taped to the ground. The first was a square, and the second was a shape known as Kanizsa square illusion. When comparing the two options given to 7 cats, 5 chose the square, and 2 chose the Kanizsa square illusion. We are interested to know whether these data provide convincing evidence that cats prefer one of the shapes over the other. (Smith, Chouinard, and Byosiere 2021)
What are the null and alternative hypotheses for evaluating whether these data provide convincing evidence that cats have preference for one of the shapes
A null hypothesis simulation (with 1,000 draws) was run, and the resulting null distribution is displayed in the histogram below. Find the p-value using this distribution and conclude the hypothesis test in the context of the problem.
-
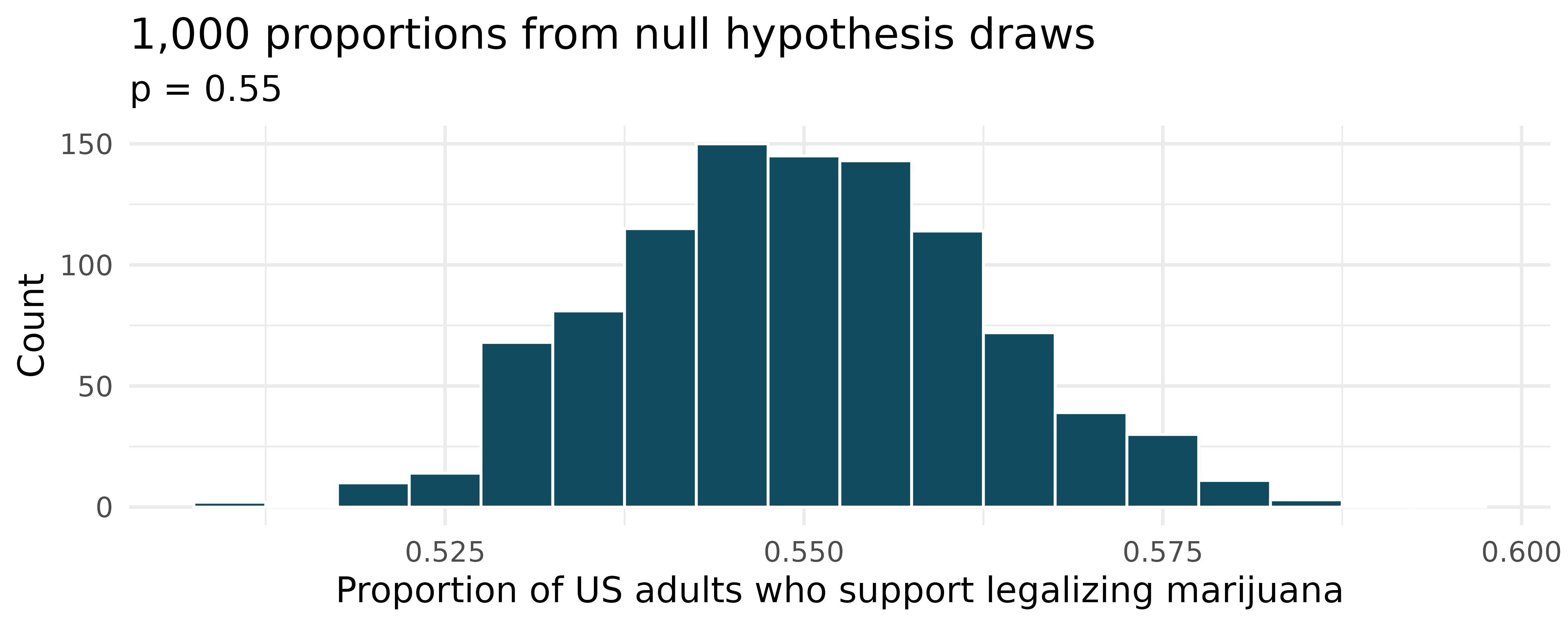
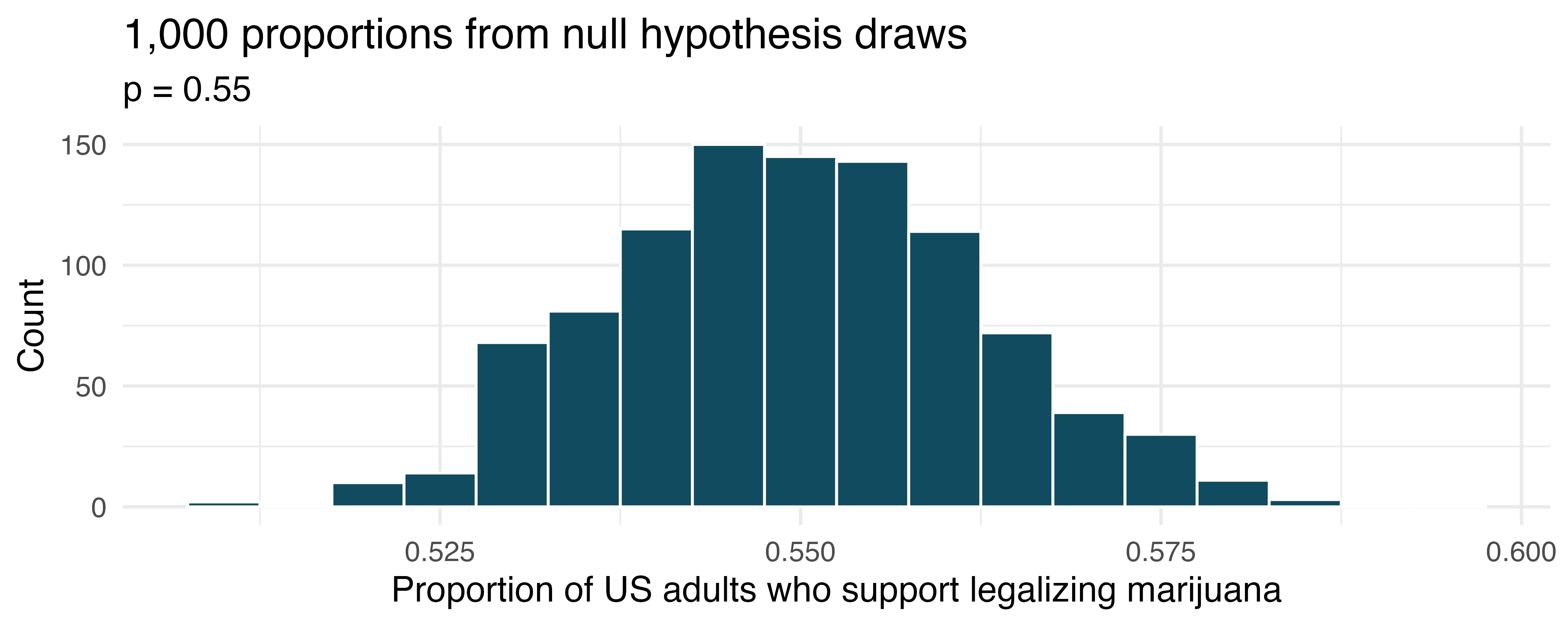
Legalization of marijuana, simulated null hypothesis. The 2022 General Social Survey asked a random sample of 1,207 US adults: “Do you think the use of marijuana should be made legal, or not?” 65.3% of the respondents said it should be made legal. (NORC 2022) Consider a scenario where, in order to become legal, 55% (or more) of voters must approve.
What are the null and alternative hypotheses for evaluating whether these data provide convincing evidence that, if voted on, marijuana would be legalized in the US.
A null hypothesis simulation (with 1,000 draws) was run, and the resulting null distribution is displayed in the histogram below. Find the p-value using this distribution and conclude the hypothesis test in the context of the problem.
-
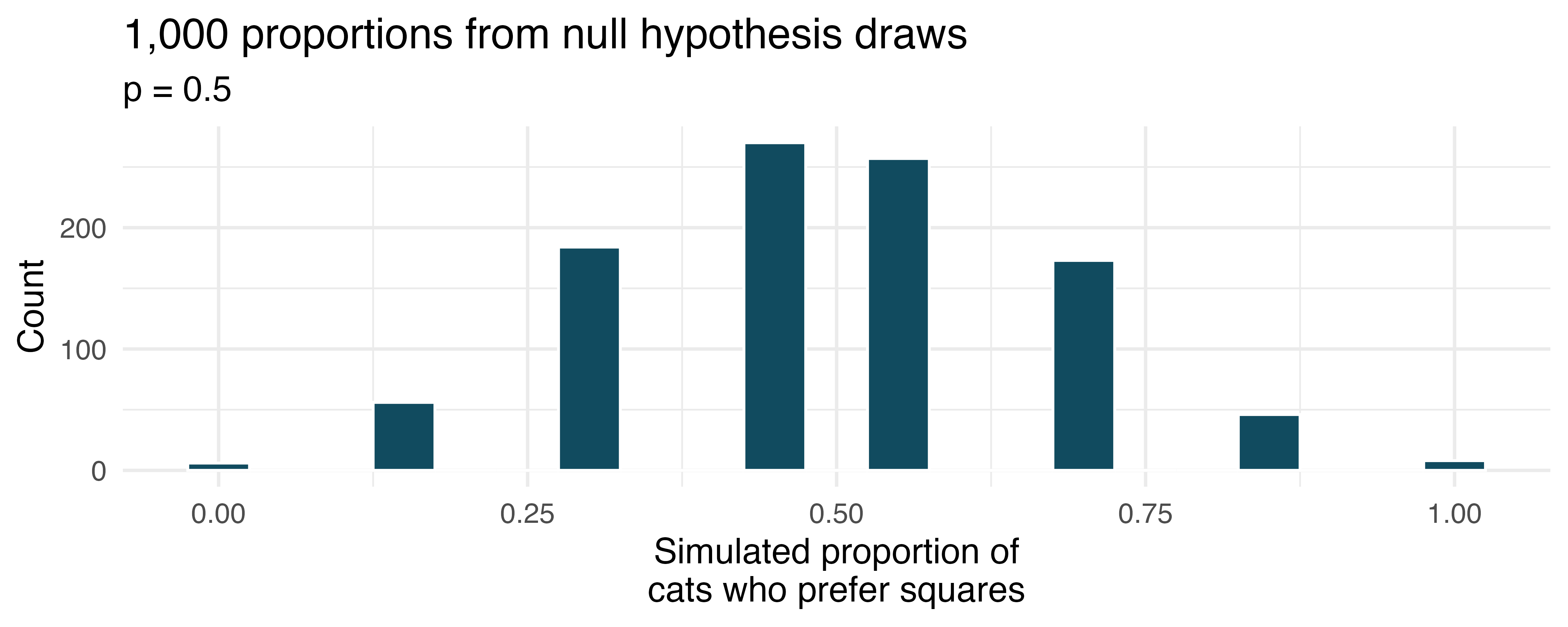
If I fits, I sits, standard errors. The results of a study on the type of enclosed spaces cats are most likely to sit in show that 5 out of 7 cats chose a square taped to the ground over a shape known as Kanizsa square illusion, which was preferred by the remaining 2 cats. To evaluate whether these data provide convincing evidence that cats prefer one of the shapes over the other, we set
Using the mathematical model, calculate the standard error of the sample proportion in repeated samples of size 7.
A null hypothesis simulation (with 1,000 draws) was run, and the resulting null distribution is displayed in the histogram below. This distribution shows the variability of the sample proportion in samples of size 7 when 50% of cats prefer the square shape over the Kanizsa square illusion. What is the approximate standard error of the sample proportion based on this distribution?
Do the mathematical model and simulated draws yield similar standard errors?
In order to approach the problem using the mathematical model, is the success-failure condition met for this study? Explain.
What features of the null distribution shown above tells us that the mathematical model should probably not be used?
-
Legalization of marijuana, standard errors. According to the 2022 General Social Survey, in a random sample of 1,207 US adults, 65.3% think marijuana should be made legal. (NORC 2022) Consider a scenario where, in order to become legal, 55% (or more) of voters must approve.
Calculate the standard error of the sample proportion using the mathematical model.
1,000 sample proportions from samples of size 1,207 were drawn from a null distribution where 55% of voters approve legalizing marijuana. The distribution of these proportions is shown in the histogram below. Approximate the standard error of the sample proportion based on this distribution.
Do the mathematical model and simulated draws yield similar standard errors?
In this setting (to test whether the true underlying population proportion is greater than 0.55), would there be a strong reason to choose the mathematical model over the simulated null hypothesis (or vice versa)?
-
Statistics and employment, describe the bootstrap. A large university knows that about 70% of the full-time students are employed at least 5 hours per week. The members of the Statistics Department wonder if the same proportion of their students work at least 5 hours per week. They randomly sample 25 majors and find that 15 of the students work 5 or more hours each week.
Two sampling distributions are created to describe the variability in the proportion of statistics majors who work at least 5 hours per week. The null hypothesis simulation imposes a true population proportion of
The sampling was done under two different settings to generate each of the distributions shown above. Describe the two different settings.
Where are each of the two distributions centered? How do their centers compare?
Estimate the standard error of the simulated proportions based on each distribution. Are the two standard errors you estimate roughly equal?
Describe the shapes of the two distributions. Are they roughly the same?
-
National Health Plan, simulated null hypothesis. A Kaiser Family Foundation poll for a random sample of US adults in 2019 found that 79% of Democrats, 55% of Independents, and 24% of Republicans supported a generic “National Health Plan”. There were 347 Democrats, 298 Republicans, and 617 Independents surveyed. (Kaiser Family Foundation 2019)
A political pundit on TV claims that a majority of Independents support a National Health Plan. Do these data provide strong evidence to support this type of statement? One approach to assessing the question of whether a majority of Independents support a National Health Plan is to simulate 1,000 draws from a null hypothesis with
The histogram above displays 1000 values of what?
Is the observed proportion of Independents consistent with the null hypothesis simulated proportions under the setting where
In order to test the claim that “a majority of Independents support a National Health Plan” what are the null and alternative hypotheses?
Using the simulated null hypothesis distribution, find the p-value and conclude the hypothesis test in the context of the problem.
-
Statistics and employment, use the bootstrap. In a large university where 70% of the full-time students are employed at least 5 hours per week, the members of the Statistics Department wonder if the same proportion of their students work at least 5 hours per week. They randomly sample 25 majors and find that 15 of the students work 5 or more hours each week.
Two sampling distributions are created to describe the variability in the proportion of statistics majors who work at least 5 hours per week. The null hypothesis distribution imposes a true population proportion of
Which distribution should be used to test whether the proportion of all statistics majors who work at least 5 hours per week is 70%? And which distribution should be used to find a confidence interval for the true poportion of statistics majors who work at least 5 hours per week?
Using the appropriate histogram, test the claim that 70% of statistics majors, like their peers, work at least 5 hours per week. State the null and alternative hypotheses, find the p-value, and conclude the test in the context of the problem.
Using the appropriate histogram, find a 98% bootstrap percentile confidence interval for the true proportion of statistics majors who work at least 5 hours per week. Interpret the confidence interval in the context of the problem.
Using the appropriate historgram, find a 98% bootstrap SE confidence interval for the true proportion of statistics majors who work at least 5 hours per week. Interpret the confidence interval in the context of the problem.
-
CLT for proportions. Define the term “sampling distribution” of the sample proportion, and describe how the shape, center, and spread of the sampling distribution change as the sample size increases when
-
Vegetarian college students. Suppose that 8% of college students are vegetarians. Determine if the following statements are true or false, and explain your reasoning.
The distribution of the sample proportions of vegetarians in random samples of size 60 is approximately normal since
The distribution of the sample proportions of vegetarian college students in random samples of size 50 is right skewed.
A random sample of 125 college students where 12% are vegetarians would be considered unusual.
A random sample of 250 college students where 12% are vegetarians would be considered unusual.
The standard error would be reduced by one-half if we increased the sample size from 125 to 250.
-
Young Americans, American dream. About 77% of young adults think they can achieve the American dream. Determine if the following statements are true or false, and explain your reasoning. (Vaughn 2011)
The distribution of sample proportions of young Americans who think they can achieve the American dream in random samples of size 20 is left skewed.
The distribution of sample proportions of young Americans who think they can achieve the American dream in random samples of size 40 is approximately normal since
A random sample of 60 young Americans where 85% think they can achieve the American dream would be considered unusual.
A random sample of 120 young Americans where 85% think they can achieve the American dream would be considered unusual.
-
Orange tabbies. Suppose that 90% of orange tabby cats are male. Determine if the following statements are true or false, and explain your reasoning.
The distribution of sample proportions of random samples of size 30 is left skewed.
Using a sample size that is 4 times as large will reduce the standard error of the sample proportion by one-half.
The distribution of sample proportions of random samples of size 140 is approximately normal.
The distribution of sample proportions of random samples of size 280 is approximately normal.
-
Young Americans, starting a family. About 25% of young Americans have delayed starting a family due to the continued economic slump. Determine if the following statements are true or false, and explain your reasoning. (Demos 2011)
The distribution of sample proportions of young Americans who have delayed starting a family due to the continued economic slump in random samples of size 12 is right skewed.
In order for the distribution of sample proportions of young Americans who have delayed starting a family due to the continued economic slump to be approximately normal, we need random samples where the sample size is at least 40.
A random sample of 50 young Americans where 20% have delayed starting a family due to the continued economic slump would be considered unusual.
A random sample of 150 young Americans where 20% have delayed starting a family due to the continued economic slump would be considered unusual.
Tripling the sample size will reduce the standard error of the sample proportion by one-third.
-
Sex equality. The General Social Survey asked a random sample of 1,390 Americans the following question: “On the whole, do you think it should or should not be the government’s responsibility to promote equality between men and women?” 82% of the respondents said it “should be”. At a 95% confidence level, this sample has 2% margin of error. Based on this information, determine if the following statements are true or false, and explain your reasoning. (NORC 2016)
We are 95% confident that 80% to 84% of Americans in this sample think it’s the government’s responsibility to promote equality between men and women.
We are 95% confident that 80% to 84% of all Americans think it’s the government’s responsibility to promote equality between men and women.
If we considered many random samples of 1,390 Americans, and we calculated 95% confidence intervals for each, 95% of these intervals would include the true population proportion of Americans who think it’s the government’s responsibility to promote equality between men and women.
In order to decrease the margin of error to 1%, we would need to quadruple (multiply by 4) the sample size.
Based on this confidence interval, there is sufficient evidence to conclude that a majority of Americans think it’s the government’s responsibility to promote equality between men and women.
-
Elderly drivers. A Marist Poll report states that 66% of American adults think licensed drivers should be required to retake their road test once they reach 65 years of age, based on a random sample of 1,018 American adults. They also report a margin of error was 3% at the 95% confidence level. (Poll 2011)
Verify the margin of error reported by The Marist Poll using a mathematical model.
Based on a 95% confidence interval, does the poll provide convincing evidence that more than two thirds of the population think that licensed drivers should be required to retake their road test once they turn 65?
-
Fireworks on July 4
-
Proof of COVID-19 vaccination. In the US, businesses and schools shut down due to the COVID-19 pandemic in March 2020, and a vaccine became publicly available for the first time in April 2021. That month, a Gallup poll surveyed a random sample of 3,731 US adults, asking how they felt about the COVID-19 vaccine requirement for air travel. The poll found that 57% said they would favor it. (Gallup 2021)
Describe the population parameter of interest. What is the value of the point estimate of this parameter?
Check if the conditions required for constructing a confidence interval using a mathematical model based on these data are met.
Construct a 95% confidence interval for the proportion of US adults who favor requiring proof of COVID-19 vaccination for travel by airplane.
Without doing any calculations, describe what would happen to the confidence interval if we decided to use a higher confidence level.
Without doing any calculations, describe what would happen to the confidence interval if we used a larger sample.
-
Study abroad. A survey on 1,509 high school seniors who took the SAT and who completed an optional web survey shows that 55% of high school seniors are fairly certain that they will participate in a study abroad program in college. (American Council on Education 2008)
Is this sample a representative sample from the population of all high school seniors in the US? Explain your reasoning.
Suppose the conditions for inference are met, regardless of your answer to part (a). Using a mathematical model, construct a 90% confidence interval for the proportion of high school seniors (of those who took the SAT) who are fairly certain they will participate in a study abroad program in college, and interpret this interval in context.
What does “90% confidence” mean?
Based on this interval, would it be appropriate to claim that the majority of high school seniors are fairly certain that they will participate in a study abroad program in college?
-
Legalization of marijuana, mathematical interval. The General Social Survey asked a random sample of 1,563 US adults: “Do you think the use of marijuana should be made legal, or not?” 60% of the respondents said it should be made legal. (NORC 2022)
Is 60% a sample statistic or a population parameter? Explain.
Using a mathematical model, construct a 95% confidence interval for the proportion of US adults who think marijuana should be made legal, and interpret it in the context of the data.
A critic points out that this 95% confidence interval is only accurate if the statistic follows a normal distribution, or if the normal model is a good approximation. Do the technical conditions hold for these data? Explain.
A news piece on this survey’s findings states, “Majority of US adults think marijuana should be legalized.” Based on your confidence interval, is the news piece’s statement justified?
-
National Health Plan, mathematical inference. A Kaiser Family Foundation poll for a random sample of US adults in 2019 found that 79% of Democrats, 55% of Independents, and 24% of Republicans supported a generic “National Health Plan”. There were 347 Democrats, 298 Republicans, and 617 Independents surveyed. (Kaiser Family Foundation 2019)
A political pundit on TV claims that a majority of Independents support a National Health Plan. Do these data provide strong evidence to support this type of statement? Your response should use a mathematical model.
Would you expect a confidence interval for the proportion of Independents who oppose the public option plan to include 0.5? Explain.
-
Is college worth it? Among a simple random sample of 331 American adults who do not have a four-year college degree and are not currently enrolled in school, 48% said they decided not to go to college because they could not afford school. (Pew Research Center 2011)
A newspaper article states that only a minority of the Americans who decide not to go to college do so because they cannot afford it and uses the point estimate from this survey as evidence. Conduct a hypothesis test to determine if these data provide strong evidence supporting this statement.
Would you expect a confidence interval for the proportion of American adults who decide not to go to college because they cannot afford it to include 0.5? Explain.
-
Taste test. Some people claim that they can tell the difference between a diet soda and a regular soda in the first sip. A researcher wanting to test this claim randomly sampled 80 such people. He then filled 80 plain white cups with soda, half diet and half regular through random assignment, and asked each person to take one sip from their cup and identify the soda as diet or regular. 53 participants correctly identified the soda.
Do these data provide strong evidence that these people are able to detect the difference between diet and regular soda, in other words, are the results discernibly better than just random guessing? Your response should use a mathematical model.
Interpret the p-value in this context.
-
Will the coronavirus bring the world closer together? In early 2020 the COVID-19 pandemic arrived in the US; by December 2020 the first COVID-19 vaccine was available. An April 2021 YouGov poll asked 4,265 UK adults whether they think the coronavirus bring the world closer together or leave us further apart. 12% of the respondents said it will bring the world closer together. 37% said it would leave us further apart, 39% said it won’t make a difference and the remainder didn’t have an opinion on the matter. (YouGov 2021)
Calculate, using a mathematical model, a 90% confidence interval for the proportion of UK adults who think the coronavirus will bring the world closer together, and interpret the interval in context.
Suppose we wanted the margin of error for the 90% confidence level to be about 0.5%. How large of a sample size would you recommend for the poll?
-
Quality control. As part of a quality control process for computer chips, an engineer at a factory randomly samples 212 chips during a week of production to test the current rate of chips with severe defects. She finds that 27 of the chips are defective.
What population is under consideration in the dataset?
What parameter is being estimated?
What is the point estimate for the parameter?
What is the name of the statistic that can be used to measure the uncertainty of the point estimate?
Compute the value of the statistic from part (d) using a mathematical model.
The historical rate of defects is 10%. Should the engineer be surprised by the observed rate of defects during the current week?
Suppose the true population value was found to be 10%. If we use this proportion to recompute the value in part (d) using
- Nearsighted children. Nearsightedness (myopia) is a common vision condition in which you can see near objects clearly, but farther away objects blurry. It is believed that nearsightedness affects about 8% of all children. In a random sample of 194 children, 21 are nearsighted. Using a mathematical model, conduct a hypothesis test for the following question: do these data provide evidence that the 8% value is inaccurate?
-
Website registration. A website is trying to increase registration for first-time visitors, exposing 1% of these visitors to a new site design. Of 752 randomly sampled visitors over a month who saw the new design, 64 registered.
Check the conditions for constructing a confidence interval for the proportion of first-time visitors of the site who would register under the new design using a mathematical model.
Compute the standard error which would describe the variability os the point estimate associated with repeated samples of size 752.
Construct and interpret a 90% confidence interval for the fraction of first-time visitors of the site who would register under the new design (assuming stable behaviors by new visitors over time).
- Coupons driving visits. A store randomly samples 603 shoppers over the course of a year and finds that 142 of them made their visit because of a coupon they’d received in the mail. Using a mathematical model, construct a 95% confidence interval for the fraction of all shoppers during the year whose visit was because of a coupon they’d received in the mail.
There is not enough evidence to reject the null hypothesis in favor of the alternative hypothesis. We cannot conclude that there is evidence that the consultant’s surgery complication rate is lower than the US standard rate of 10%. That said, we also cannot conclude that there is evidence that the consultant’s surgery complication rate is higher than the US standard rate of 10%. When the p-value is larger than the discernibility level, we are unable to make conclusions about the research statement.↩︎
Not necessarily. There is no evidence to make a claim in either direction, so we cannot make any claims about whether the consultant is good at their job.↩︎
Because the
This is equivalent to asking how often the
Since the necessary conditions for applying the normal model have already been checked for us, we can go straight to the construction of the confidence interval:
We must find
Note, the problem was set up as 90% to indicate that there was not a need for a high level of confidence (such as 95% or 99%). A lower degree of confidence increases potential for error, but it also produces a more narrow interval.↩︎Independence holds since the poll is based on a random sample. The success-failure condition also holds, which is checked using the null value