Appendix A — Exercise solutions

A.1 Chapter 1

23 observations and 7 variables.
(a) “Is there an association between air pollution exposure and preterm births?” (b) 143,196 births in Southern California between 1989 and 1993. (c) Measurements of carbon monoxide, nitrogen dioxide, ozone, and particulate matter less than 10$\mu g/m^3$ (PM$_{10}$) collected at air-quality-monitoring stations as well as length of gestation. Continuous numerical variables.
(a) “What is the effect of gamification on learning outcomes compared to traditional teaching methods?” (b) 365 college students taking a statistics course (c) Gender (categorical), level of studies (categorical, ordinal), academic major (categorical), expertise in English language (categorical, ordinal), use of personal computers and games (categorical, ordinal), treatment group (categorical), score (numerical, discrete).
(a) Treatment: $10/43 = 0.23 \rightarrow 23\%$. (b) Control: $2/46 = 0.04 \rightarrow 4\%$. (c) A higher percentage of patients in the treatment group were pain free 24 hours after receiving acupuncture. (d) It is possible that the observed difference between the two group percentages is due to chance. (e) Explanatory: acupuncture or not. Response: if the patient was pain free or not.
(a) Experiment; researchers are evaluating the effect of fines on parents’ behavior related to picking up their children late from daycare. (b) 10 cases: the daycare centers. (c) Number of late pickups (discrete numerical). (d) Week (numerical, discrete), group (categorical, nominal), number of late pickups (numerial, discrete), and study period (categorical, ordinal).
(a) 344 cases (penguins) are included in the data. (b) There are 4 numerical variables in the data: bill length, bill depth, and flipper length (measured in millimeters) and body mass (measured in grams). They are all continuous. (c) There are 3 categorical variables in the data: species (Adelie, Chinstrap, Gentoo), island (Torgersen, Biscoe, and Dream), and sex (female and male).
(a) Airport ownership status (public/private), airport usage status (public/private), region (Central, Eastern, Great Lakes, New England, Northwest Mountain, Southern, Southwest, Western Pacific), latitude, and longitude. (b) Airport ownership status: categorical, not ordinal. Airport usage status: categorical, not ordinal. Region: categorical, not ordinal. Latitude: numerical, continuous. Longitude: numerical, continuous.
(a) Year, number of baby girls named Fiona born in that year, nation. (b) Year (numerical, discrete), number of baby girls named Fiona born in that year (numerical, discrete), nation (categorical, nominal).
(a) County, state, driver’s race, whether the car was searched or not, and whether the driver was arrested or not. (b) All categorical, non-ordinal. (c) Response: whether the car was searched or not. Explanatory: race of the driver.
(a) Observational study. (b) Dog: Lucy. Cat: Luna. (c) Oliver and Lily. (d) Positive, as the popularity of a name for dogs increases, so does the popularity of that name for cats.

A.2 Chapter 2

(a) Population mean, $\mu_{2007} = 52$; sample mean, $\bar{x}_{2008} = 58$. (b) Population mean, $\mu_{2001} = 3.37$; sample mean, $\bar{x}_{2012} = 3.59$.
(a) Population: all births, sample: 143,196 births between 1989 and 1993 in Southern California. (b) If births in this time span at the geography can be considered to be representative of all births, then the results are generalizable to the population of Southern California. However, since the study is observational the findings cannot be used to establish causal relationships.
(a) The population of interest is all college students studying statistics. The sample consists of 365 such students. (b) If the students in this sample, who are likely not randomly sampled, can be considered to be representative of all college students studying statistics, then the results are generalizable to the population defined above. This is probably not a reasonable assumption since these students are from two specific majors only. Additionally, since the study is experimental, the findings can be used to establish causal relationships.
(a) Observation. (b) Variable. (c) Sample statistic (mean). (d) Population parameter (mean).
(a) Observational. (b) Use stratified sampling to randomly sample a fixed number of students, say 10, from each section for a total sample size of 40 students.
(a) Positive, non-linear, somewhat strong. Countries in which a higher percentage of the population have access to the internet also tend to have higher average life expectancies, however rise in life expectancy trails off before around 80 years old. (b) Observational. (c) Wealth: countries with individuals who can widely afford the internet can probably also afford basic medical care. (Note: Answers may vary.)
(a) Simple random sampling is okay. In fact, it’s rare for simple random sampling to not be a reasonable sampling method! (b) The student opinions may vary by field of study, so the stratifying by this variable makes sense and would be reasonable. (c) Students of similar ages are probably going to have more similar opinions, and we want clusters to be diverse with respect to the outcome of interest, so this would not be a good approach. (Additional thought: the clusters in this case may also have very different numbers of people, which can also create unexpected sample sizes.)
(a) The cases are 200 randomly sampled men and women. (b) The response variable is attitude towards a fictional microwave oven. (c) The explanatory variable is dispositional attitude. (d) Yes, the cases are sampled randomly, recruited online using Amazon’s Mechanical Turk. (e) This is an observational study since there is no random assignment to treatments. (f) No, we cannot establish a causal link between the explanatory and response variables since the study is observational. (g) Yes, the results of the study can be generalized to the population at large since the sample is random.
(a) Simple random sample. Non-response bias, if only those people who have strong opinions about the survey responds their sample may not be representative of the population. (b) Convenience sample. Under coverage bias, their sample may not be representative of the population since it consists only of their friends. It is also possible that the study will have non-response bias if some choose to not bring back the survey. (c) Convenience sample. This will have a similar issues to handing out surveys to friends. (d) Multi-stage sampling. If the classes are similar to each other with respect to student composition this approach should not introduce bias, other than potential non-response bias.
(a) Exam performance. (b) Light level: fluorescent overhead lighting, yellow overhead lighting, no overhead lighting (only desk lamps). (c) Wearing glasses or not.
(a) Experiment. (b) Light level (overhead lighting, yellow overhead lighting, no overhead lighting) and noise level (no noise, construction noise, and human chatter noise). (c) Since the researchers want to ensure equal representation of those wearing glasses and not wearing glasses, wearing glasses is a blocking variable.
Need randomization and blinding. One possible outline: (1) Prepare two cups for each participant, one containing regular Coke and the other containing Diet Coke. Make sure the cups ar identical and contain equal amounts of soda. Label the cups (regular) and B (diet). (Be sure to randomize A and B for each trial!) (2) Give each participant the two cups, one cup at a time, in random order, and ask the participant to record a value that indicates ho much she liked the beverage. Be sure that neither the participant nor the person handing out the cups knows the identity of th beverage to make this a double-blind experiment. (Answers may vary.)
(a) Experiment. (b) Treatment: 25 grams of chia seeds twice a day, control: placebo. (c) Yes, gender. (d) Yes, single blind since the patients were blinded to the treatment they received. (e) Since this is an experiment, we can make a causal statement. However, since the sample is not random, the causal statement cannot be generalized to the population at large.
(a) Non-responders may have a different response to this question, e.g., parents who returned the surveys likely don’t have difficulty spending time with their children. (b) It is unlikely that the women who were reached at the same address 3 years later are a random sample. These missing responders are probably renters (as opposed to homeowners) which means that they might have a lower socio-economic status than the respondents. (c) There is no control group in this study, this is an observational study, and there may be confounding variables, e.g., these people may go running because they are generally healthier and/or do other exercises.
(a) Randomized controlled experiment. (b) Explanatory: treatment group (categorical, with 3 levels). Response variable: Psychological well-being. (c) No, because the participants were volunteers. (d) Yes, because it was an experiment. (e) The statement should say “evidence” instead of “proof”.

A.3 Chapter 3

Application chapter, no exercises.

A.4 Chapter 4

(a) We see the order of the categories and the relative frequencies in the bar plot. (b) There are no features that are apparent in the pie chart but not in the bar plot. (c) We usually prefer to use a bar plot as we can also see the relative frequencies of the categories in this graph.
(a) The horizontal locations at which the age groups break into the various opinion levels differ, which indicates that likelihood of supporting protests varies by age group. Two variables may be associated. (b) Answers may vary. Political ideology/leaning and education level.
(a) Number of participants in each group. (b) Proportion of survival. (c) The standardized bar plot should be displayed as a way to visualize the survival improvement in the treatment versus the control group.
(a) The ridge plots do not tell us about the relationship between meat consumption and life expectancy. While it is true that the high income group of countries has highest meat consumption and highest life expectancy, we can’t, for example, differentiate meat consumption across the low and middle income groups (so as to connect to life expectancy). Additionally, we don’t know anything about the relationship betwen meat consumption and life expectancy within an income group. (b) When a relationship is confounded we cannot determine the causal mechanism. We don’t know if the longer life expecancy is due to meat consumption or due to higher income (which comes with many other life-extending practices). (c) In order to investigate a specific confounding variable, first break the data into categories according to that confounding variable (here, income). Then look at the relationship of interest (here meat consumption and life expectancy) separately for each of the levels of the confounding variable (income).
(a) 41% of the JetBlue flights are delayed. 40.7% of the United Airlines flights are delayed. (b) For SFO: JetBlue had 39.7% delayed, United had 40% delayed (United had more delayed flights). For LAX: JetBlue had 40.1% delayed, United had 41% delayed (United had more delayed flights). For BQN: JetBlue had 45.7% delayed, United had 48.8% delayed (United had more delayed flights). (c) Note that JetBlue had substantially more flights than United out of BQN (where there was a high delay percentage). United had substantially more flights than United out of SFO and LAX, both of which had low delay percentages. So JetBlue’s overall percentage delay is bumped up due to the BQN flights, and United’s overall percentage delay is bumped down due to the SFO and LAX flights.

A.5 Chapter 5

(a) Positive association: mammals with longer gestation periods tend to live longer as well. (b) Association would still be positive. (c) No, they are not independent. See part (a).
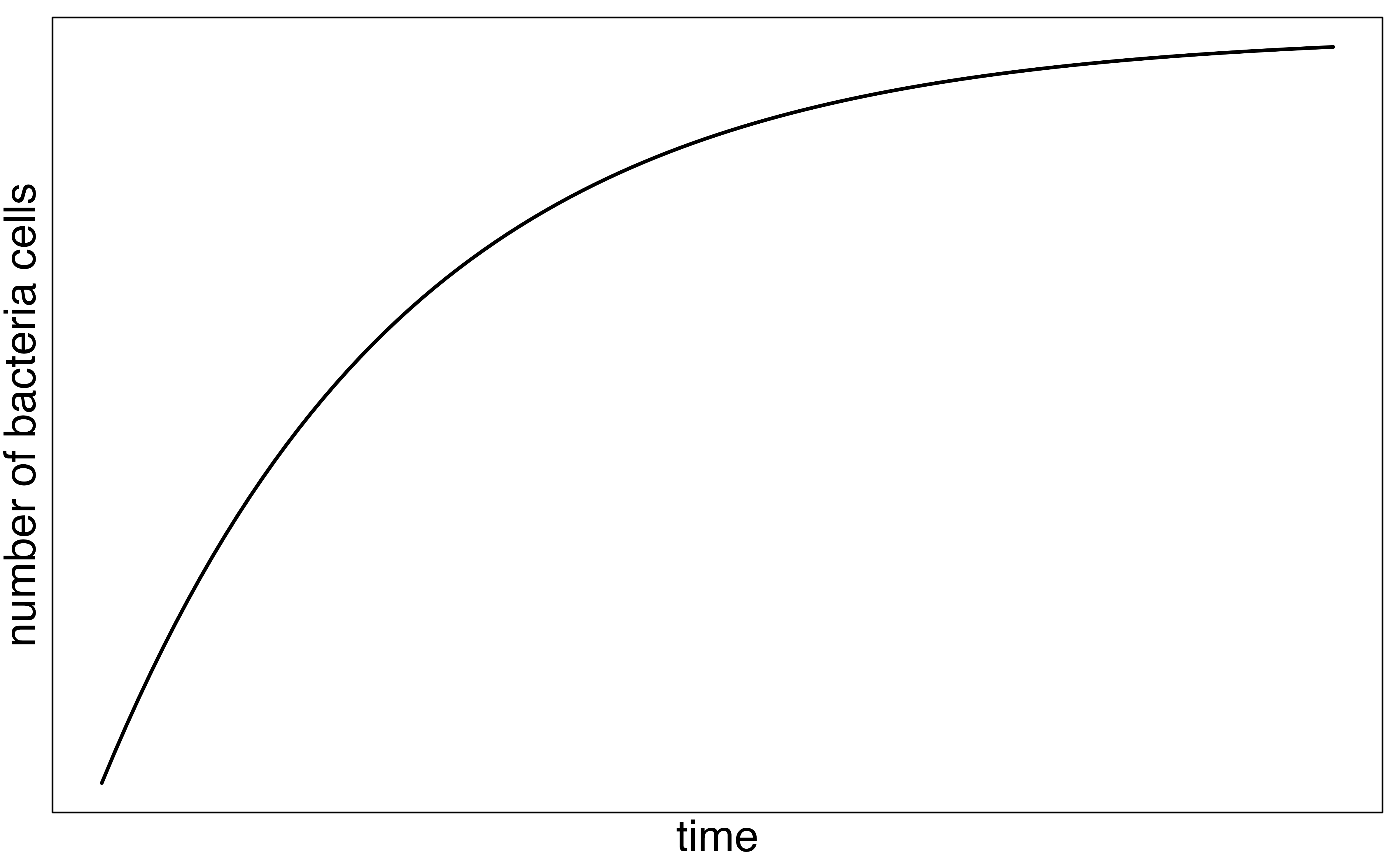
The graph below shows a ramp up period. There may also be a period of exponential growth at the start before the size of the petri dish becomes a factor in slowing growth.
(a) Decrease: the new score is smaller than the mean of the 24 previous scores. (b) Calculate a weighted mean. Use a weight of 24 for the old mean and 1 for the new mean: $(24\times 74 + 1\times64)/(24+1) = 73.6$. (c) The new score is more than 1 standard deviation away from the previous mean, so increase.
Any 10 employees whose average number of days off is between the minimum and the mean number of days off for the entire workforce at this plant.
(a) Dist B has a higher mean since $20 > 13$, and a higher standard deviation since 20 is further from the rest of the data than 13. (b) Dist A has a higher mean since $-20 > -40$, and Dist B has a higher standard deviation since -40 is farther away from the rest of the data than -20. (c) Dist B has a higher mean since all values in this Dist Are higher than those in Dist A, but both distribution have the same standard deviation since they are equally variable around their respective means. (d) Both distributions have the same mean since they’re both centered at 300, but Dist B has a higher standard deviation since the observations are farther from the mean than in Dist A.
(a) About 26. (b) Since the distribution is right skewed the mean is higher than the median. (c) Q1: between 15 and 20, Q3: between 35 and 40, IQR: about 20. (d) Values that are considered to be unusually low or high lie more than 1.5$\times$IQR away from the quartiles. Upper fence: Q3 + 1.5 $\times$ IQR = $37.5 + 1.5 \times 20 = 67.5$; Lower fence: Q1 - 1.5 $\times$ IQR = $17.5 + 1.5 \times 20 = -12.5$; The lowest AQI recorded is not lower than 5 and the highest AQI recorded is not higher than 65, which are both within the fences. Therefore none of the days in this sample would be considered to have an unusually low or high AQI.
The histogram shows that the distribution is bimodal, which is not apparent in the box plot. The box plot makes it easy to identify more precise values of observations outside of the whiskers.
(a) Right skewed, there is a natural boundary at 0 and only a few people have many pets. Center: median, variability: IQR. (b) Right skewed, there is a natural boundary at 0 and only a few people live a very long distance from work. Center: median, variability: IQR. (c) Symmetric. Center: mean, variability: standard deviation. (d) Left skewed. Center: median, variability: IQR. (e) Left skewed. Center: median, variability: IQR.
No, we would expect this distribution to be right skewed. There are two reasons for this: there is a natural boundary at 0 (it is not possible to watch less than 0 hours of TV) and the standard deviation of the distribution is very large compared to the mean.
No, the outliers are likely the maximum and the minimum of the distribution so a statistic based on these values cannot be robust to outliers.
The 75th percentile is 82.5, so 5 students will get an A. Also, by definition 25% of students will be above the 75th percentile.
(a) If $\frac{\bar{x}}{median} = 1$, then $\bar{x} = median$. This is most likely to be the case for symmetric distributions. (b) If $\frac{\bar{x}}{median} < 1$, then $\bar{x} < median$. This is most likely to be the case for left skewed distributions, since the mean is affected (and pulled down) by the lower values more so than the median. (c) If $\frac{\bar{x}}{median} > 1$, then $\bar{x} > median$. This is most likely to be the case for right skewed distributions, since the mean is affected (and pulled up) by the higher values more so than the median.
(a) The distribution of percentage of population that is Hispanic is extremely right skewed with majority of counties with less than 10% Hispanic residents. However there are a few counties that have more than 90% Hispanic population. It might be preferable to, in certain analyses, to use the log-transformed values since this distribution is much less skewed. (b) The map reveals that counties with higher proportions of Hispanic residents are clustered along the Southwest border, all of New Mexico, a large swath of Southwest Texas, the bottom two-thirds of California, and in Southern Florida. In the map all counties with more than 40% of Hispanic residents are indicated by the darker shading, so it is impossible to discern how high Hispanic percentages go. The histogram reveals that there are counties with over 90% Hispanic residents. The histogram is also useful for estimating measures of center and spread. (c) Both visualizations are useful, but if we could only examine one, we should examine the map since it explicitly ties geographic data to each county’s percentage.

A.6 Chapter 6

Application chapter, no exercises.

A.7 Chapter 7

(a) The residual plot will show randomly distributed residuals around 0. The variance is also approximately constant. (b) The residuals will show a fan shape, with higher variability for smaller $x$. There will also be many points on the right above the line. There is trouble with the model being fit here.
(a) Strong relationship, but a straight line would not fit the data. (b) Strong relationship, and a linear fit would be reasonable. (c) Weak relationship, and trying a linear fit would be reasonable. (d) Moderate relationship, but a straight line would not fit the data. (e) Strong relationship, and a linear fit would be reasonable. (f) Weak relationship, and trying a linear fit would be reasonable.
(a) Exam 2 since there is less of a scatter in the plot of course grade versus exam 2. Notice that the relationship between Exam 1 and the course grade appears to be slightly nonlinear. (b) (Answers may vary.) If Exam 2 is cumulative it might be a better indicator of how a student is doing in the class.
(a) $r = -0.7$ $\rightarrow$ (4). (b) $r = 0.45$ $\rightarrow$ (3). (c) $r = 0.06$ $\rightarrow$ (1). (d) $r = 0.92$ $\rightarrow$ (2).
(a) There is a moderate, positive, and linear relationship between shoulder girth and height. (b) Changing the units, even if just for one of the variables, will not change the form, direction or strength of the relationship between the two variables.
(a) There is a somewhat weak, positive, possibly linear relationship between the distance traveled and travel time. There is clustering near the lower left corner that we should take special note of. (b) Changing the units will not change the form, direction or strength of the relationship between the two variables. If longer distances measured in miles are associated with longer travel time measured in minutes, longer distances measured in kilometers will be associated with longer travel time measured in hours. (c) Changing units doesn’t affect correlation: $r = 0.636$.
we can write the amount of meat consumption as an exact linear function of the amount of carbohydrate consumption. (a) $carbs = meat - 3.$ (b) $carbs = meat + 2.$ (c) $carbs = 2 \times meat.$ Since the slopes are positive and these are perfect linear relationships, the correlation will be exactly 1 in all three parts. An alternative way to gain insight into this solution is to create a mock dataset, e.g., 5 countries with meat consumption of 10, 20, 50, 75, and 100 kg per capita, find the related carbohydrate consumption for each mock country, then create a scatterplot.
Correlation: no units. Intercept: cal. Slope: cal/cm.
Over-estimate. Since the residual is calculated as $observed - predicted$, a negative residual means that the predicted value is higher than the observed value.
(a) There is a positive, moderate, linear association between number of calories and amount of carbohydrates. In addition, the amount of carbohydrates is more variable for menu items with higher calories, indicating non-constant variance. There also appear to be two clusters of data: a patch of about a dozen observations in the lower left and a larger patch on the right side. (b) Explanatory: number of calories. Response: amount of carbohydrates (in grams). (c) With a regression line, we can predict the amount of carbohydrates for a given number of calories. This may be useful if only calorie counts for the food items are posted but the amount of carbohydrates in each food item is not readily available. (d) Food menu items with higher predicted protein are predicted with higher variability than those without, suggesting that the model is doing a better job predicting protein amount for food menu items with lower predicted proteins.
(a) First calculate the slope: $b_1 = R\times s_y/s_x = 0.636 \times 113 / 99 = 0.726$. Next, make use of the fact that the regression line passes through the point $(\bar{x},\bar{y})$: $\bar{y} = b_0 + b_1 \times \bar{x}$. Plug in $\bar{x}$, $\bar{y}$, and $b_1$, and solve for $b_0$: 51. Solution: $\widehat{travel~time} = 51 + 0.726 \times distance$. (b) $b_1$: For each additional mile in distance, the model predicts an additional 0.726 minutes in travel time. $b_0$: When the distance travelled is 0 miles, the travel time is expected to be 51 minutes. It does not make sense to have a travel distance of 0 miles in this context. Here, the $y$-intercept serves only to adjust the height of the line and is meaningless by itself. (c) $R^2 = 0.636^2 = 0.40$. About 40% of the variability in travel time is accounted for by the model, i.e., explained by the distance travelled. (d) $\widehat{travel~time} = 51 + 0.726 \times distance = 51 + 0.726 \times 103 \approx 126$ minutes. (Note: we should be cautious in our predictions with this model since we have not yet evaluated whether it is a well-fit model.) (e) $e_i = y_i - \hat{y}_i = 168 - 126 = 42$ minutes. A positive residual means that the model underestimates the travel time. (f) No, this calculation would require extrapolation.
(a) $\widehat{\texttt{poverty}} = 4.60 + 2.05 \times \texttt{unemployment\_rate}.$ (b) The model predicts a poverty rate of 4.60% for counties with 0% unemployment, on average. This is not a meaningful value as no counties have such low unexmployment, it just serves to adjust the height of the regression line. (c) For each additional percentage increase in unemployment rate, poverty rate is predicted to be higher, on average, by 2.05%. (d) Unemployment rate explains 46% of the variability in poverty levels in US counties. (e) $\sqrt{0.46} = 0.678.$
(a) There is an outlier in the bottom right. Since it is far from the center of the data, it is a point with high leverage. It is also an influential point since, without that observation, the regression line would have a very different slope. (b) There is an outlier in the bottom right. Since it is far from the center of the data, it is a point with high leverage. However, it does not appear to be affecting the line much, so it is not an influential point. (c) The observation is in the center of the data (in the x-axis direction), so this point does not have high leverage. This means the point won’t have much effect on the slope of the line and so is not an influential point.
(a) There is a negative, moderate-to-strong, somewhat linear relationship between percent of families who own their home and the percent of the population living in urban areas in 2010. There is one outlier: a state where 100% of the population is urban. The variability in the percent of homeownership also increases as we move from left to right in the plot. (b) The outlier is located in the bottom right corner, horizontally far from the center of the other points, so it is a point with high leverage. It is an influential point since excluding this point from the analysis would greatly affect the slope of the regression line.
(a) True. (b) False, correlation is a measure of the linear association between any two numerical variables.
(a) $r = 0.7 \to (1)$ (b) $r = 0.09 \to (4)$ (c) $r = -0.91 \to (2)$ (d) $r = 0.96 \to (3)$.

A.8 Chapter 8

Annika is right. All variables being highly correlated, including the predictor variables being highly correlated with each other, is not desirable as this would result in multicollinearity.
(a) The association between meat consumption and life expectancy is positive, moderate, and curved. (b) While tempting to say that eating meat may lead to a longer life expectancy, we do not have any sense of why the variables are associated. We are better off thinking that the countries with high meat consumption and high life expectancy are similar in many other ways (e.g., income bracket). (c) Within an income bracket, the relationship between meat consumption and life expectancy is not nearly as strong (as compared to when the data are aggregated into one plot).
No, they shouldn’t include all variables as days_since_start and days_since_race are perfectly correlated with each other. They should only include one of them.
(a) $\widehat{\texttt{weight}} = 7.270 - 0.593 \times \texttt{habit}_\texttt{smoker}$. (b) The estimated body weight of babies born to smoking mothers is 0.593 pounds lower than those who are born to non-smoking mothers. Smoker: $\widehat{\texttt{weight}} = 7.270 - 0.593 \times 1 = 6.68$ pounds. Non-smoker: $\widehat{\texttt{weight}} = 7.270 - 0.593 \times 0 = 7.270$ pounds.
(a) Horror movies. (b) Not necessarily, the change in adjusted $R^2$ is quite small.
(a) $\widehat{\texttt{weight}} = -3.82 + 0.26 \times \texttt{weeks} + 0.02 \times \texttt{mage} + 0.37 \times \texttt{sex}_\texttt{male} + 0.02 \times \texttt{visits} - 0.43 \times \texttt{habit}_\texttt{smoker}.$ (b) $b_{\texttt{weeks}}$: The model predicts a 0.26 pound increase in the birth weight of the baby for each additional week in length of pregnancy, all else held constant. $b_{\texttt{habit}_\texttt{smoker}}$: The model predicts a 0.43 pound decrease in the birth weight of the babies born to smoker mothers compared to non-smokers, all else held constant. (c) Habit might be correlated with one of the other variables in the model, which introduces multicollinearity and complicates model estimation. (d) -0.17~lbs.
Remove gained.
Add weeks.

A.9 Chapter 9

(a) False. The line is fit to predict the probability of success, not the binary outcome. (b) False. Residuals are not used in logistic regression like they are in linear regression because the observed value is always either zero or one (and the predicted value is a probability). The goal of the logistic regression is not to get a perfect prediction (of zero or one), so minimizing residuals is not part of the modeling process. (c) True.
(a) There are a few potential outliers, e.g., on the left in the variable total length, but nothing that will be of serious concern in a dataset this large. (b) When coefficient estimates are sensitive to which variables are included in the model, this typically indicates that some variables are collinear. For example, a possum’s gender may be related to its head length, which would explain why the coefficient for sex changed when we removed the variable. Likewise, a possum’s skull width is likely to be related to its head length and probably even much more closely related than the head length was to gender.
(a) The logistic model relating $\hat{p}$ to the predictors may be written as $\log\left( \frac{\hat{p}}{1 - \hat{p}} \right) = 33.5095 - 1.4207\times \texttt{sex}_{\texttt{male}} - 0.2787 \times \texttt{skull\_w} + 0.5687 \times \texttt{total\_l} - 1.8057 \times \texttt{tail\_l}.$ Only total_l has a positive association with a possum being from Victoria. (b) $\hat{p} = 0.0062$. While the probability is very near zero, we have not run diagnostics on the model. We might also be a little skeptical that the model will remain accurate for a possum found in a US zoo. For example, perhaps the zoo selected a possum with specific characteristics but only looked in one region. On the other hand, it is encouraging that the possum was caught in the wild. (Answers regarding the reliability of the model probability will vary.)
(a) The variable exclaim_subj should be removed, since it’s removal reduces AIC the most (and the resulting model has lower AIC than the None Dropped model). (b) The variable cc should be removed. (c) Removing any variable will increase AIC, so we should not remove any variables from this set.
(a) The AIC is smallest using the variables sex, head_l, skull_w, total_l, and tail_l to predict region (AIC = 83.52), so we would choose that model. (b) If the metric is equivalent across two models with different numbers of variables, we usually want the model with smaller number of variables. Sometimes refered to as Occam’s razor, the simplest explanation is often the one that will generalize most effectively.

A.10 Chapter 10

Application chapter, no exercises.

A.11 Chapter 11

(a) Mean. Each student reports a numerical value: a number of hours. (b) Mean. Each student reports a number, which is a percentage, and we can average over these percentages. (c) Proportion. Each student reports Yes or No, so this is a categorical variable and we use a proportion. (d) Mean. Each student reports a number, which is a percentage like in part (b). (e) Proportion. Each student reports whether s/he expects to get a job, so this is a categorical variable and we use a proportion.
(a) Alternative. (b) Null. (c) Alternative. (d) Alternative. (e) Null. (f) Alternative. (g) Null.
(a) $H_0: \mu = 8$ (On average, New Yorkers sleep 8 hours a night.) $H_A: \mu < 8$ (On average, New Yorkers sleep less than 8 hours a night.) (b) $H_0: \mu = 15$ (The average amount of company time each employee spends not working is 15 minutes for March Madness.) $H_A: \mu > 15$ (The average amount of company time each employee spends not working is greater than 15 minutes for March Madness.)
(a) (i) False. Instead of comparing counts, we should compare percentages of people in each group who suffered cardiovascular problems. (ii) True. (iii) False. Association does not imply causation. We cannot infer a causal relationship based on an observational study. The difference from part (ii) is subtle. (iv) True. (b) Proportion of all patients who had cardiovascular problems: $\frac{7,979}{227,571} \approx 0.035$ (c) The expected number of heart attacks in the Rosiglitazone group, if having cardiovascular problems and treatment were independent, can be calculated as the number of patients in that group multiplied by the overall cardiovascular problem rate in the study: $67,593 * \frac{7,979}{227,571} \approx 2370$. (d) (i) $H_0$: The treatment and cardiovascular problems are independent. They have no relationship, and the difference in incidence rates between the Rosiglitazone and Pioglitazone groups is due to chance. $H_A$: The treatment and cardiovascular problems are not independent. The difference in the incidence rates between the Rosiglitazone and Pioglitazone groups is not due to chance and Rosiglitazone is associated with an increased risk of serious cardiovascular problems. (ii) A higher number of patients with cardiovascular problems than expected under the assumption of independence would provide support for the alternative hypothesis as this would suggest that Rosiglitazone increases the risk of such problems. (iii) In the actual study, we observed 2,593 cardiovascular events in the Rosiglitazone group. In the 100 simulations under the independence model, the simulated differences were never so high, which suggests that the actual results did not come from the independence model. That is, the variables do not appear to be independent, and we reject the independence model in favor of the alternative. The study’s results provide convincing evidence that Rosiglitazone is associated with an increased risk of cardiovascular problems.

A.12 Chapter 12

(a) The statistic is the sample proportion (0.289); the parameter is the population proportion (unknown). (b) $\hat{p}$ and $p$. (c) Bootstrap sample proportion. (d) 0.289. (e) Roughly (0.22, 0.35). (f) We can be 90% confident that between 22% and 35% of all YouTube videos take place outdoors.
With 98% confidence, the true proportion of all US adults (in 2022) who get news from social media sometimes or often is between 0.487 and 0.51.
(a) A or perhaps D. (b) A, B, C, or D. (c) B or C. (d) B. (e) None.
(a) This claim is reasonable, since the entire interval lies above 50%. (b) The value of 70% lies outside of the interval, so we have convincing evidence that the researcher’s conjecture is wrong. (c) A 90% confidence interval will be narrower than a 95% confidence interval. Even without calculating the interval, we can tell that 70% would not fall in the interval, and we would reject the researcher’s conjecture based on a 90% confidence level as well.

A.13 Chapter 13

(a) 0.089 (b) 0.069 (c) 0.589 (d) $P(|Z| > 2) = P(Z < -2) + P(Z > 2)$ 0.046
(a) Verbal: $N(\mu = 151, \sigma = 7)$, Quant: $N(\mu = 153, \sigma = 7.67)$. (b) $Z_{VR} = 1.29$, $Z_{QR} = 0.52$. (c) She scored 1.29 standard deviations above the mean on the Verbal Reasoning section and 0.52 standard deviations above the mean on the Quantitative Reasoning section.

She did better on the Verbal Reasoning section since her Z score on that section was higher. (e)$Perc_{VR} = 0.9007 \approx 90\%$, $Perc_{QR} = 0.6990 \approx 70\%$. (f) $100\% - 90\% = 10\%$ did better than her on VR, and $100\% - 70\% = 30\%$ did better than her on QR. (g) We cannot compare the raw scores since they are on different scales. Comparing her percentile scores is more appropriate when comparing her performance to others. (h) Answer to part (b) would not change as Z scores can be calculated for distributions that are not normal. However, we could not answer parts (d)-(f) since we cannot use the normal probability table to calculate probabilities and percentiles without a normal model.

(a) $Z = 0.84$, which corresponds to approximately 159 on QR. (b) $Z = -0.52$, which corresponds to approximately 147 on VR.
(a) $Z = 1.2$, $P(Z > 1.2) = 0.1151$. (b) $Z= -1.28 \to 70.6\circ$F or colder.
(a) $N(25, 2.78)$. (b) $Z = 1.08$, $P(Z > 1.08) = 0.1401$. (c)The answers are very close because only the units were changed. (The only reason why they differ at all because 28$^\circ$ C is 82.4$^\circ$ F, not precisely 83$^\circ$ F.) (d) Since $IQR = Q3 - Q1$, we first need to find $Q3$ and $Q1$ and take the difference between the two. Remember that $Q3$ is the $75^{th}$ and $Q1$ is the $25^{th}$ percentile of a distribution. Q1 = 23.13, Q3 = 26.86, IQR = 26. 86 - 23.13 = 3.73.
(a) Recall that the general formula is $point~estimate \pm z^{\star} \times SE$. First, identify the three different values. The point estimate is 45%, $z^{\star} = 1.96$ for a 95% confidence level, and $SE = 1.2\%$. Then, plug the values into the formula: $45\% \pm 1.96 \times 1.2\% \quad\to\quad (42.6\%, 47.4\%)$ We are 95% confident that the proportion of US adults who live with one or more chronic conditions is between 42.6% and 47.4%. (b) (i) False. Confidence intervals provide a range of plausible values, and sometimes the truth is missed. A 95% confidence interval “misses” about 5% of the time. (ii) True. Notice that the description focuses on the true population value. (iii) True. If we examine the 95% confidence interval, we can see that 50% is not included in this interval. This means that in a hypothesis test, we would reject the null hypothesis that the proportion is 0.5. (iv) False. The standard error describes the uncertainty in the overall estimate from natural fluctuations due to randomness, not the uncertainty corresponding to individuals’ responses.
A Z score of 0.47 denotes that the sample proportion is 0.47 standard errors greater than the hypothesized value of the population proportion.
(a) Sampling distribution. (b) To know whether the distribution is skewed, we need to know the proportion. We’ve been told the proportion is likely above 5% and below 30%, and the success-failure condition would be satisfied for any of these values. If the population proportion is in this range, the sampling distribution will be symmetric. (c) Standard error. (d) The distribution will tend to be more variable when we have fewer observations per sample.

A.14 Chapter 14

(a) $H_0$: Anti-depressants do not affect the symptoms of Fibromyalgia. $H_A$: Anti-depressants do affect the symptoms of Fibromyalgia (either helping or harming). (b) Concluding that anti-depressants either help or worsen Fibromyalgia symptoms when they actually do neither. (c) Concluding that anti-depressants do not affect Fibromyalgia symptoms when they actually do.
(a) Scenario (i) is higher. Recall that a sample mean based on less data tends to be less accurate and have larger standard errors. (b) Scenario (i) is higher. The higher the confidence level, the higher the corresponding margin of error. (c) They are equal. The sample size does not affect the calculation of the p-value for a given Z score. (d) Scenario (i) is higher. If the null hypothesis is harder to reject (lower $\alpha$), then we are more likely to make a Type II error when the alternative hypothesis is true.
The hypotheses should be about the population proportion ($p$), not the sample proportion. The null hypothesis should have an equal sign. The alternative hypothesis should have a not-equals sign, and it should reference the null value, $p_0 = 0.6$, not the observed sample proportion. The correct way to set up these hypotheses is: $H_0: p = 0.6$ and $H_A: p \neq 0.6$.
Regardless of whether the students were making 95% intervals or 90% intervals, seven students with intervals that miss $\pi$ seems totally reasonable. The students should not be docked for the intervals missing $\pi$.
True. If the sample size gets ever larger, then the standard error will become ever smaller. Eventually, when the sample size is large enough and the standard error is tiny, we can find statistically discernible yet very small differences between the null value and point estimate (assuming they are not exactly equal).

A.15 Chapter 15

Application chapter, no exercises.

A.16 Chapter 16

First, the hypotheses should be about the population proportion ($p$), not the sample proportion. Second, the null value should be what we are testing (0.25), not the observed value (0.29). The correct way to set up these hypotheses is: $H_0: p = 0.25$ and $H_A: p > 0.25.$
(a) $H_0 : p = 0.20,$ $H_A : p > 0.20.$ (b) $\hat{p} = 159/650 = 0.245.$ (c) Answers will vary. Each student can be represented with a card. Take 100 cards, 20 black cards representing those who support proposals to defund police departments and 80 red cards representing those who do not. Shuffle the cards and draw with replacement (shuffling each time in between draws) 650 cards representing the 650 respondents to the poll. Calculate the proportion of black cards in this sample, $\hat{p}_{sim},$ i.e., the proportion of those who upport proposals to defund police departments. The p-value will be the proportion of simulations where $\hat{p}_{sim} \geq 0.245.$ (Note: We would generally use a computer to perform the simulations.) (d) There 1 only one simulated proportion that is at least 0.245, therefore the approximate p-value is 0.001. Your p-value may vary slightly since it is based on a visual estimate. Since the p-value is smaller than 0.05, we reject $H_0.$ The data provide convincing evidence that the proportion of Seattle adults who support proposals to defund police departments is greater than 0.20, i.e., more than one in five.
(a) $H_0: p = 0.5$, $H_A: p \ne 0.5$. (b) The p-value is roughly 0.4, There is not evidence in the data (possibly because there are only 7 cats being measured!) to conclude that the cats have a preference one way or the other between the two shapes.
(a) $SE(\hat{p}) = 0.189$. (c) Roughly 0.188. (c) Yes. (d) No. (e) The draws from the null hypothesis are discrete (only a few distinct options) and the mathematical model is continuous (infinite options on a continuum).
(a) The null hypothesis simulation was done with $p=0.7$, and the data bootstrap simulation was done with $p = 0.6.$ (b) The null hypothesis simulation is centered at 0.7; the data bootstrap is centered at 0.6. (c) The standard error of the sample proportion is given to be roughly 0.1 for both histograms. (d) Both histograms are reasonably symmetric. Note that histograms which describe the variability of proportions become more skewed as the center of the distribution gets closer to 1 (or zero) because the boundary of 1.0 restricts the symmetry of the tail of the distribution. For this reason, the null hypothesis simulation histogram is slightly more skewed (left).
(a) The null hypothesis simulation distribution for testing. The data bootstrap distribution for confidence intervals. (b) $H_0: p = 0.7;$ $H_A: p \ne 0.7.$ p-value $> 0.05.$ There is no evidence that the proportion of full-time statistics majors who work is different from 70%. (c) We are 98% confident that the true proportion of all full-time student statistics majors who work at least 5 hours per week is between 35% and 80%. (d) Using $z^\star = 2.33$, the 98% confidence interval is 0.367 to 0.833.
(a) False. Doesn’t satisfy success-failure condition. (b) True. The success-failure condition is not satisfied. In most samples we would expect $\hat{p}$ to be close to 0.08, the true population proportion. While $\hat{p}$ can be much above 0.08, it is bound below by 0, suggesting it would take on a right skewed shape. Plotting the sampling distribution would confirm this suspicion. (c) False. $SE_{\hat{p}} = 0.0243$, and $\hat{p} = 0.12$ is only $\frac{0.12 - 0.08}{0.0243} = 1.65$ SEs away from the mean, which would not be considered unusual. (d) True. $\hat{p}=0.12$ is 2.32 standard errors away from the mean, which is often considered unusual. (e) False. Decreases the SE by a factor of $1/\sqrt{2}$.
(a) True. See the reasoning of 6.1(b). (b) True. We take the square root of the sample size in the SE formula. (c) True. The independence and success-failure conditions are satisfied. (d) True. The independence and success-failure conditions are satisfied.
(a) False. A confidence interval is constructed to estimate the population proportion, not the sample proportion. (b) True. 95% CI: $82\%\ \pm\ 2\%$. (c) True. By the definition of the confidence level. (d) True. Quadrupling the sample size decreases the SE and ME by a factor of $1/\sqrt{4}$. (e) True. The 95% CI is entirely above 50%.
With a random sample, independence is satisfied. The success-failure condition is also satisfied. $ME = z^{\star} \sqrt{ \frac{\hat{p} (1-\hat{p})} {n} } = 1.96 \sqrt{ \frac{0.56 \times 0.44}{600} }= 0.0397 \approx 4\%.$
(a) No. The sample only represents students who took the SAT, and this was also an online survey. (b) (0.5289, 0.5711). We are 90% confident that 53% to 57% of high school seniors who took the SAT are fairly certain that they will participate in a study abroad program in college. (c) 90% of such random samples would produce a 90% confidence interval that includes the true proportion. (d) Yes. The interval lies entirely above 50%.
(a) We want to check for a majority (or minority), so we use the following hypotheses: $H_0: p = 0.5$ and $H_A: p \neq 0.5$. We have a sample proportion of $\hat{p} = 0.55$ and a sample size of $n = 617$ independents. Since this is a random sample, independence is satisfied. The success-failure condition is also satisfied: $617 \times 0.5$ and $617 \times (1 - 0.5)$ are both at least 10 (we use the null proportion $p_0 = 0.5$ for this check in a one-proportion hypothesis test). Therefore, we can model $\hat{p}$ using a normal distribution with a standard error of $SE = \sqrt{\frac{p(1 - p)}{n}} = 0.02$. (We use the null proportion $p_0 = 0.5$ to compute the standard error for a one-proportion hypothesis test.) Next, we compute the test statistic: $Z = \frac{0.55 - 0.5}{0.02} = 2.5.$ This yields a one-tail area of 0.0062, and a p-value of $2 \times 0.0062 = 0.0124.$ Because the p-value is smaller than 0.05, we reject the null hypothesis. We have strong evidence that the support is different from 0.5, and since the data provide a point estimate above 0.5, we have strong evidence to support this claim by the TV pundit. (b) No. Generally we expect a hypothesis test and a confidence interval to align, so we would expect the confidence interval to show a range of plausible values entirely above 0.5. However, if the confidence level is misaligned (e.g., a 99% confidence level and a $\alpha = 0.05$ discernibility level), then this is no longer generally true.
(a) $H_0: p = 0.5$. $H_A: p > 0.5$. Independence (random sample, $<10\%$ of population) is satisfied, as is the success-failure conditions (using $p_0 = 0.5$, we expect 40 successes and 40 failures). $Z = 2.91$ $\to$ p- value $= 0.0018$. Since the p-value $< 0.05$, we reject the null hypothesis. The data provide strong evidence that the rate of correctly identifying a soda for these people is discernibly better than just by random guessing. (b) If in fact people cannot tell the difference between diet and regular soda and they randomly guess, the probability of getting a random sample of 80 people where 53 or more identify a soda correctly would be 0.0018.
(a) The sample is from all computer chips manufactured at the factory during the week of production. We might be tempted to generalize the population to represent all weeks, but we should exercise caution here since the rate of defects may change over time. (b) The fraction of computer chips manufactured at the factory during the week of production that had defects. (c) Estimate the parameter using the data: $\hat{p} = \frac{27}{212} = 0.127$. (d) Standard error (or $SE$). (e) Compute the $SE$ using $\hat{p} = 0.127$ in place of $p$: $SE \approx \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}} = \sqrt{\frac{0.127(1 - 0.127)}{212}} = 0.023$. (f) The standard error is the standard deviation of $\hat{p}$. A value of 0.10 would be about one standard error away from the observed value, which would not represent a very uncommon deviation. (Usually beyond about 2 standard errors is a good rule of thumb.) The engineer should not be surprised. (g) Recomputed standard error using $p = 0.1$: $SE = \sqrt{\frac{0.1(1 - 0.1)}{212}} = 0.021$. This value isn’t very different, which is typical when the standard error is computed using relatively similar proportions (and even sometimes when those proportions are quite different!).
(a) The visitors are from a simple random sample, so independence is satisfied. The success-failure condition is also satisfied, with both 64 and $752 - 64 = 688$ above 10. Therefore, we can use a normal distribution to model $\hat{p}$ and construct a confidence interval. (b) The sample proportion is $\hat{p} = \frac{64}{752} = 0.085$. The standard error is $SE = \sqrt{\frac{0.085 (1 - 0.085)}{752}} = 0.010.$ (c) For a 90% confidence interval, use $z^{\star} = 1.65$. The confidence interval is $0.085 \pm 1.65 \times 0.010 \to (0.0685, 0.1015)$. We are 90% confident that 6.85% to 10.15% of first-time site visitors will register using the new design.

A.17 Chapter 17

(a) The parameter is $p_{Asican-Indian} - p_{Chinese}.$ The statistic is $\hat{p}_{Asian-Indian} - \hat{p}_{Chinese} = 223/4373 - 279/4736 = -0.008$ (b) Roughly 0.005. (c) $H_0: p_{Asian-Indian} - p_{Chinese} = 0;$, $H_A: p_{Asian-Indian} - p_{Chinese} \ne 0.$ The evidence is borderline but worth further study. There is not strong evidence that the true difference in proportion of current smokers is different across the two ethnic groups.
(a) Roughly 0.00625. (b) We are 95% confident that the true proportion of Filipino Americans who are current smokers is between 5.28 and 7.72 percentage points higher in the control vaccine group than the proportion of Chinese Americans who smoke. (c) We are 95% confident that the true proportion of Filipino Americans who are current smokers is between 5.2 and 7.7 percentage points higher in the control vaccine group than the proportion of Chinese Americans who smoke.
(a) While the standard errors of the difference in proportion across the two graphs are roughly the same (approximately 0.012), the centers are not. Computational method A is centered at 0.07 (the difference in the observed sample proportions) and Computational method B is centered at 0. (b) What is the difference between the proportions of Bachelor’s and Associate’s students who believe that the COVID-19 pandemic will negatively impact their ability to complete the degree? (c) Is the proportion of Bachelor’s students who believe that their ability to complete the degree will be negatively impacted by the COVID-19 pandemic different than that of Associate’s students?
(a) 26 Yes and 94 No in Nevaripine and 10 Yes and 110 No in Lopinavir group. (b) $H_0: p_N = p_L$. There is no difference in virologic failure rates between the Nevaripine and Lopinavir groups. $H_A: p_N \ne p_L$. There is some difference in virologic failure rates between the Nevaripine and Lopinavir groups. (c) Random assignment was used, so the observations in each group are independent. If the patients in the study are representative of those in the general population (something impossible to check with the given information), then we can also confidently generalize the findings to the population. The success-failure condition, which we would check using the pooled proportion ($\hat{p}_{pool} = 36/240 = 0.15$), is satisfied. $Z = 2.89$ $\to$ p-value $=0.0039$. Since the p-value is low, we reject $H_0$. There is strong evidence of a difference in virologic failure rates between the Nevaripine and Lopinavir groups. Treatment and virologic failure do not appear to be independent.
(a) Standard error: $SE = \sqrt{\frac{0.79(1 - 0.79)}{347} + \frac{0.55(1 - 0.55)}{617}} = 0.03.$ Using $z^{\star} = 1.96$, we get: $0.79 - 0.55 \pm 1.96 \times 0.03 \to (0.181, 0.299).$ We are 95% confident that the proportion of Democrats who support the plan is 18.1% to 29.9% higher than the proportion of Independents who support the plan. (b) True.
(a) In effect, we’re checking whether men are paid more than women (or vice-versa), and we’d expect these outcomes with either chance under the null hypothesis: $H_0: p = 0.5$ and $H_A: p \neq 0.5.$ We’ll use $p$ to represent the fraction of cases where men are paid more than women. (b) There isn’t a good way to check independence here since the jobs are not a simple random sample. However, independence doesn’t seem unreasonable, since the individuals in each job are different from each other. The success-failure condition is met since we check it using the null proportion: $p_0 n = (1 - p_0) n = 10.5$ is greater than 10. We can compute the sample proportion, $SE$, and test statistic: $\hat{p} = 19 / 21 = 0.905$ and $SE = \sqrt{\frac{0.5 \times (1 - 0.5)}{21}} = 0.109$ and $Z = \frac{0.905 - 0.5}{0.109} = 3.72.$ The test statistic $Z$ corresponds to an upper tail area of about 0.0001, so the p-value is 2 times this value: 0.0002. Because the p-value is smaller than 0.05, we reject the notion that all these gender pay disparities are due to chance. Because we observe that men are paid more in a higher proportion of cases and we have rejected $H_0$, we can conclude that men are being paid higher amounts in ways not explainable by chance alone. If you’re curious for more info around this topic, including a discussion about adjusting for additional factors that affect pay, please see the following video by Healthcare Triage: youtu.be/aVhgKSULNQA.
Before we can calculate a confidence interval, we must first check that the conditions are met. There aren’t at least 10 successes and 10 failures in each of the four groups (treatment/control and yawn/not yawn), $(\hat{p}_C - \hat{p}_T)$ is not expected to be approximately normal and therefore cannot calculate a confidence interval for the difference between the proportions of participants who yawned in the treatment and control groups using large sample techniques and a critical Z score.
(a) False. The confidence interval includes 0. (b) False. We are 95% confident that 16% fewer to 2% Americans who make less than $40,000 per year are not at all personally affected by the government shutdown compared to those who make $40,000 or more per year. (c) False. As the confidence level decreases the width of the confidence level decreases as well. (d) True.
(a) Type I. (b) Type II. (c) Type II.
No. The samples at the beginning and at the end of the semester are not independent since the survey is conducted on the same students.
(a) The proportion of the normal curve centered at -0.1 with a standard deviation of 0.15 that is less than -2 * standard error is 0.09. (b) The proportion of the normal curve centered at -0.4 with a standard deviation of 0.145 that is less than 2 * standard error is 0.78. (c) The proportion of the normal curve centered at -0.1 with a standard deviation of 0.0671 that is less than 2 * standard error is 0.31. (d) The proportion of the normal curve centered at -0.4 with a standard deviation of 0.0678 that is less than 2 * standard error is 1. (e) The larger the value of $\delta$ and the larger the sample size, the more likely that the future study will lead to sample proportions which are able to reject the null hypothesis.

A.18 Chapter 18

(a) Two-way table is shown below. (b-i) $E_{row_1, col_1} = \frac{(row~1~total)\times(col~1~total)}{table~total} = 35$. This is lower than the observed value. (b-ii) $E_{row_2, col_2} = \frac{(row~2~total)\times(col~2~total)}{table~total} = 115$. This is lower than the observed value.

Quit

Treatment Yes No Total

Patch + support group 40 110 150

Only patch 30 120 150

Total 70 230 300
(a) Sun = 0.343, Partial = 0.325, Shade = 0.331. (b) For each, the numbers are listed in the order sun, partial, and shade: Desert (40,9, 38,7, 39.4), Mountain (36.7, 34.8, 35.5), Valley (36.4, 34.5, 35.1). (c) Yes. (d) We can’t evaluate the association without a formal test.
The original dataset will have a higher Chi-squared statistic than the randomized dataset.
(a) The two variables are independent. (b) The randomized Chi-squared values range from zero to approximately 15. (c) The null hypothesis is that the variables are independent; the alternative hypothesis is that the variables are associated. The p-value is extremely small. The habitat provides information about the likelihood of being in the different sunshine states.
(a) The two variables are independent. (b) The randomized Chi-squared values range from zero to approximately 25. (c) The null hypothesis is that the variables are independent; the alternative hypothesis is that the variables are associated. The p-value is around 0. There is convincing evidence to claim that site and sunlight preference are associated. (d) With larger sample sizes, the power (the probability of rejecting $H_0$ when $H_A$ is true) is higher.
(a) False. The Chi-square distribution has one parameter called degrees of freedom. (b) True. (c) True. (d) False. As the degrees of freedom increases, the shape of the Chi-square distribution becomes more symmetric.
The hypotheses are $H_0:$ Sleep levels and profession are independent. $H_A:$ Sleep levels and profession are associated. The observations are independent and the sample sizes are large enough to conduct a Chi-square test of independence. The Chi-square statistic is 1 with 2 degrees of freedom. The p-value is 0.6. Since the p-value is high (default to alpha = 0.05), we fail to reject $H_0$. The data do not provide convincing evidence of an association between sleep levels and profession.
(a) $H_0$: The age of Los Angeles residents is independent of shipping carrier preference variable. $H_A$: The age of Los Angeles residents is associated with the shipping carrier preference variable. (b) The conditions are not satisfied since some expected counts are below 5.

	Quit
Patch + support group	40	110	150
Only patch	30	120	150
Total	70	230	300

A.19 Chapter 19

(a) Average sleep of 20 in sample vs. all New Yorkers. (b) Average height of students in study vs all undergraduates.
(a) Use the sample mean to estimate the population mean: 171.1. Likewise, use the sample median to estimate the population median: 170.3. (b) Use the sample standard deviation (9.4) and sample IQR ($177.8-163.8 = 14$). (c) $Z_{180} = 0.95$ and $Z_{155} = -1.71.$ Neither of these observations is more than two standard deviations away from the mean, so neither would be considered unusual. (d) No, sample point estimates only estimate the population parameter, and they vary from one sample to another. Therefore we cannot expect to get the same mean and standard deviation with each random sample. (e) We use the standard error of the mean to measure the variability in means of random samples of same size taken from a population. The variability in the means of random samples is quantified by the standard error. Based on this sample, $SE_{\bar{x}} = \frac{9.4}{\sqrt{507}} = 0.417.$
(a) The kindergartners will have a smaller standard deviation of heights. We would expect their heights to be more similar to each other compared to a group of adults’ heights. (b) The standard error of the mean will depend on the variability of individual heights. The standard error of the adult sample averages will be around 9.4/$\sqrt{100}$ = 0.94cm. The standard error of the kindergartner sample averages will be smaller.
(a) $df=6-1=5$, $t_{5}^{\star} = 2.02$. (b) $df=21-1=20$, $t_{20}^{\star} = 2.53$. (c) $df=28$, $t_{28}^{\star} = 2.05$. (d) $df=11$, $t_{11}^{\star} = 3.11$.
(a) 0.085, do not reject $H_0$. (b) 0.003, reject $H_0$. (c) 0.438, do not reject $H_0$. (d) 0.042, reject $H_0$.
(a) Roughly 0.1 weeks. (b) Roughly (38.45 weeks, 38.85 weeks). (c) Roughly (38.49 weeks, 38.91 weeks).
(a) False (b) False. (c) True. (d) False.
The mean is the midpoint: $\bar{x} = 20$. Identify the margin of error: $ME = 1.015$, then use $t^{\star}_{35} = 2.03$ and $SE = s/ \sqrt{n}$ in the formula for margin of error to identify $s = 3$.
(a) $H_0$: $\mu = 8$ (New Yorkers sleep 8 hrs per night on average.) $H_A$: $\mu \neq 8$ (New Yorkers sleep less or more than 8 hrs per night on average.) (b) Independence: The sample is random. The min/max suggest there are no concerning outliers. $T = -1.75$. $df=25-1=24$. (c) p-value $= 0.093$. If in fact the true population mean of the amount New Yorkers sleep per night was 8 hours, the probability of getting a random sample of 25 New Yorkers where the average amount of sleep is 7.73 hours per night or less (or 8.27 hours or more) is 0.093. (d) Since p-value $>$ 0.05, do not reject $H_0$. The data do not provide strong evidence that New Yorkers sleep more or less than 8 hours per night on average. (e) Yes, since we did not rejected $H_0$.
With a larger critical value, the confidence interval ends up being wider. This makes intuitive sense as when we have a small sample size and the population standard deviation is unknown, we should have a wider interval than if we knew the population standard deviation, or if we had a large enough sample size.
(a) We will conduct a 1-sample $t$-test. $H_0$: $\mu = 5$. $H_A$: $\mu \neq 5$. We’ll use $\alpha = 0.05$. This is a random sample, so the observations are independent. To proceed, we assume the distribution of years of piano lessons is approximately normal. $SE = 2.2 / \sqrt{20} = 0.4919$. The test statistic is $T = (4.6 - 5) / SE = -0.81$. $df = 20 - 1 = 19$. The one-tail area is about 0.21, so the p-value is about 0.42, which is bigger than $\alpha = 0.05$ and we do not reject $H_0$. That is, we do not have sufficiently strong evidence to reject the notion that the average is 5 years. (b) Using $SE = 0.4919$ and $t_{df = 19}^{\star} = 2.093$, the confidence interval is (3.57, 5.63). We are 95% confident that the average number of years a child takes piano lessons in this city is 3.57 to 5.63 years. (c) They agree, since we did not reject the null hypothesis and the null value of 5 was in the $t$-interval.

A.20 Chapter 20

The hypotheses should use population means ($\mu$) not sample means ($\bar{x}$), the null hypothesis should set the two population means equal to each other, the alternative hypothesis should be two-tailed and use a not equal to sign.
$H_0: \mu_{0.99} = \mu_{1}$ and $H_A: \mu_{0.99} \ne \mu_{1}.$ p-value $<$ 0.05, reject $H_0.$ The data provide convincing evidence that the difference in population averages of price per carat of 0.99 carats and 1 carat diamonds are different.
(a) We are 95% confident that the population average price per carat of 0.99 carat diamonds is $2 to $23 lower than the population average price per carat of 1 carat diamonds. (b) We are 95% confident that the population average price per carat of 0.99 carat diamonds is $2.91 to $21.10 lower than the population average price per carat of 1 carat diamonds.
The difference is not zero (statistically discernible), but there is no evidence that the difference is large (practically important), because the interval provides values as low as 1 lb.
$H_0: \mu_{0.99} = \mu_{1}$ and $H_A: \mu_{0.99} \ne \mu_{1}$. Independence: Both samples are random and represent less than 10% of their respective populations. Also, we have no reason to think that the 0.99 carats are not independent of the 1 carat diamonds since they are both sampled randomly. Normality: The distributions are not extremely skewed, hence we can assume that the distribution of the average differences will be nearly normal as well. $T_{22} = -2.7$, p-value = 0.0131. Since p-value less than 0.05, reject $H_0$. The data provide convincing evidence that the difference in population averages of price per carat of 0.99 carats and 1 carat diamonds are different.
We are 95% confident that the population average price per carat of 0.99 carat diamonds is $2.96 to $22.42 lower than the population average price per carat of 1 carat diamonds.
(a) $\mu_{\bar{x}_1} = 15$, $\sigma_{\bar{x}_1} = 20 / \sqrt{50} = 2.8284.$ (b) $\mu_{\bar{x}_2} = 20$, $\sigma_{\bar{x}_1} = 10 / \sqrt{30} = 1.8257.$ (c) $\mu_{\bar{x}_2 - \bar{x}_1} = 20 - 15 = 5$, $\sigma_{\bar{x}_2 - \bar{x}_1} = \sqrt{\left(20 / \sqrt{50}\right)^2 + \left(10 / \sqrt{30}\right)^2} = 3.3665.$ (d) Think of $\bar{x}_1$ and $\bar{x}_2$ as being random variables, and we are considering the standard deviation of the difference of these two random variables, so we square each standard deviation, add them together, and then take the square root of the sum: $SD_{\bar{x}_2 - \bar{x}_1} = \sqrt{SD_{\bar{x}_2}^2 + SD_{\bar{x}_1}^2}.$
(a) Chicken fed linseed weighed an average of 218.75 grams while those fed horsebean weighed an average of 160.20 grams. Both distributions are relatively symmetric with no apparent outliers. There is more variability in the weights of chicken fed linseed. (b) $H_0: \mu_{ls} = \mu_{hb}$. $H_A: \mu_{ls} \ne \mu_{hb}$. We leave the conditions to you to consider. $T=3.02$, $df = min(11, 9) = 9$ $\to$ p-value $= 0.014$. Since p-value $<$ 0.05, reject $H_0$. The data provide strong evidence that there is a discernible difference between the average weights of chickens that were fed linseed and horsebean. (c) Type I error, since we rejected $H_0$. (d) Yes, since p-value $>$ 0.01, we would not have rejected $H_0$.
$H_0: \mu_C = \mu_S$. $H_A: \mu_C \ne \mu_S$. $T = 3.27$, $df=11$ $\to$ p-value $= 0.007$. Since p-value $< 0.05$, reject $H_0$. The data provide strong evidence that the average weight of chickens that were fed casein is different than the average weight of chickens that were fed soybean (with weights from casein being higher). Since this is a randomized experiment, the observed difference can be attributed to the diet.
$H_0: \mu_{T} = \mu_{C}$. $H_A: \mu_{T} \ne \mu_{C}$. $T=2.24$, $df=21$ $\to$ p-value $= 0.036$. Since p-value $<$ 0.05, reject $H_0$. The data provide strong evidence that the average food consumption by the patients in the treatment and control groups are different. Furthermore, the data indicate patients in the distracted eating (treatment) group consume more food than patients in the control group.

A.21 Chapter 21

Paired, data are recorded in the same cities at two different time points. The temperature in a city at one point is not independent of the temperature in the same city at another time point
(a) Since it’s the same students at the beginning and the end of the semester, there is a pairing between the datasets, for a given student their beginning and end of semester grades are dependent. (b) Since the subjects were sampled randomly, each observation in the men’s group does not have a special correspondence with exactly one observation in the other (women’s) group. (c) Since it’s the same subjects at the beginning and the end of the study, there is a pairing between the datasets, for a subject student their beginning and end of semester artery thickness are dependent. (d) Since it’s the same subjects at the beginning and the end of the study, there is a pairing between the datasets, for a subject student their beginning and end of semester weights are dependent.
False. While it is true that paired analysis requires equal sample sizes, only having the equal sample sizes isn’t, on its own, sufficient for doing a paired test. Paired tests require that there be a special correspondence between each pair of observations in the two groups.
(a) Let $diff = 2022 - 1950$. Then the hypotheses are $H_0: \mu_{diff} = 0$ and $H_A: \mu_{diff} \ne 0$. (b) The observed average of difference is outside the randomized differences. (c) Since the p-value $<$ 0.05, reject $H_0$. There is evidence of a difference between the average 90$^{th}$ percentile high temperature in 2022 and the average 90$^{th}$ percentile high temperature in 1950.
(a) Roughly (1.5$^\circ$F, 3.5$^\circ$F). (b) Roughly (1.5$^\circ$F, 3.56$^\circ$F). (c) We are 90% confident that the true average of the difference in 90$^{th}$ percentile high temperature in 2022 vs 1950 is somewhere between 1.5$^\circ$F and 3.5$^\circ$F. We are 90% confident that the true average of the difference in 90$^{th}$ percentile high temperature in 2022 vs 1950 is somewhere between 1.5$^\circ$F and 3.56$^\circ$F. (d) There is a discernible difference.
(a) For each observation in the 1950 dataset, there is exactly one specially corresponding observation in the 2022 dataset for the same geographic location. The data are paired. (b) $H_0: \mu_{\text{diff}} = 0$ (There is no difference in the 90$^{th}$ percentile high temperature in 1950 and 2022 for NOAA stations.) $H_A: \mu_{\text{diff}} \neq 0$ (There is a difference.) (c) Locations were not randomly sampled across the geographic region, so we need to be careful concluding independence. However, the question above describes the data as representative of the land area of the lower 48 states, so independence is reasonable. The sample size is 26 which is close to 30, so we’re just looking for particularly extreme outliers: none are present (the observation off to the right in the histogram would be considered a outlier, but not a particularly extreme one). Therefore, the conditions are reasonably satisfied. (d) $SE = 2.95 / \sqrt{26} = 0.579$. $T = \frac{2.53 - 0}{0.579} = 4.37$ with degrees of freedom $df = 26 - 1 = 25$, which leads to a one-tail area of 0.0000954 and a p-value of about 0.0002. (e) Since the p-value is less than 0.05, we reject $H_0$. The data provide strong evidence that NOAA stations observed a hotter 90$^{th}$ percentile high temperature in 2022 than in 1950. (f) Type I error, since we may have incorrectly rejected $H_0$. This error would mean that NOAA stations did not actually observe an increase, but the sample we took just so happened to make it appear that this was the case. (g) No, since we rejected $H_0$, which had a null value of 0.
(a) $SE = 0.579$ and $t^{\star}_{25} = 1.71$. $2.53 \pm 1.71 \times 0.579 \to (1.54$^{$F, 3.52$}$F)$. (b) We are 90% confident that the true average of the difference in 90$^{th}$ percentile high temperature in 2022 vs 1950 is somewhere between 1.54$^\circ$F and 3.52$^\circ$F. (c) Yes, since the interval lies entirely above 0.
(a) Each student study under each condition, use the difference in individual student scores. (b) Each student study under one condition, use the difference in average across the two conditions.
(a)$H_0: \mu_{diff} = 0$. $H_A: \mu_{diff} \ne 0$. $T=-2.71$. $df=5$. p-value $= 0.042$. Since p-value $<$ 0.05, reject $H_0$. The data provide strong evidence that the average number of traffic accident related emergency room admissions are different between Friday the 6$^{\text{th}}$ and Friday the 13$^{\text{th}}$. Furthermore, the data indicate that the direction of that difference is that accidents are lower on Friday the $6^{th}$ relative to Friday the 13$^{\text{th}}$. (b) (-6.49, -0.17). (c) This is an observational study, not an experiment, so we cannot so easily infer a causal intervention implied by this statement. It is true that there is a difference. However, for example, this does not mean that a responsible adult going out on Friday the $13^{th}$ has a higher chance of harm than on any other night.

A.22 Chapter 22

Alternative.
(a) Means across original data are more variable. (b) Standard deviation of egg lengths are about the same for both plots. (c) F statistic is bigger for the original data.
$H_0$: $\mu_1 = \mu_2 = \cdots = \mu_6$. $H_A$: The average weight varies across some (or all) groups. Independence: Chicks are randomly assigned to feed types (presumably kept separate from one another), therefore independence of observations is reasonable. Approx. normal: the distributions of weights within each feed type appear to be fairly symmetric. Constant variance: Based on the side-by-side box plots, the constant variance assumption appears to be reasonable. There are differences in the actual computed standard deviations, but these might be due to chance as these are quite small samples. $F_{5,65} = 15.36$ and the p-value is approximately 0. With such a small p-value, we reject $H_0$. The data provide convincing evidence that the average weight of chicks varies across some (or all) feed supplement groups.
(a) $H_0$: The population mean of MET for each group is equal to the others. $H_A$: At least one pair of means is different. (b) Independence: We don’t have any information on how the data were collected, so we cannot assess independence. To proceed, we must assume the subjects in each group are independent. In practice, we would inquire for more details. Normality: The data are bound below by zero and the standard deviations are larger than the means, indicating very strong skew. However, since the sample sizes are extremely large, even extreme skew is acceptable. Constant variance: This condition is sufficiently met, as the standard deviations are reasonably consistent across groups. (c) Since p-value is very small, reject $H_0$. The data provide convincing evidence that the average MET differs between at least one pair of groups.
(a) $H_0$: Average GPA is the same for all majors. $H_A$: At least one pair of means are different. (b) Since p-value $>$ 0.05, fail to reject $H_0$. The data do not provide convincing evidence of a difference between the average GPAs across three groups of majors. (c) The total degrees of freedom is $195 + 2 = 197$, so the sample size is $197+1=198$.
(a) False. As the number of groups increases, so does the number of comparisons and hence the modified discernibility level decreases. (b) True. (c) True. (d) False. We need observations to be independent regardless of sample size.
(a) Left is Dataset B. (b) Right is Dataset A.

A.23 Chapter 23

Application chapter, no exercises.

A.24 Chapter 24

(a) $H_0: \beta_1 = 0$, $H_A: \beta_1 \ne 0$. (b) The observed slope of 0.604 is not a plausible value, the p-value is extremely small, and the null hypothesis can be rejected. c. The p-value is also extremely small.
(a) The relationship is positive, moderate-to-strong, and linear. There are a few outliers but no points that appear to be influential. (b) $\widehat{\texttt{wgt}} = -105.0113 + 1.0176 \times \texttt{hgt}$. Slope: For each additional centimeter in height, the model predicts the average weight to be 1.0176 additional kilograms (about 2.2 pounds). Intercept: People who are 0 centimeters tall are expected to weigh -105.0113 kilograms. This is obviously not possible. Here, the $y$- intercept serves only to adjust the height of the line and is meaningless by itself. (c) $H_0$: The true slope coefficient of height is zero ($\beta_1 = 0$). $H_A$: The true slope coefficient of height is different than zero ($\beta_1 \neq 0$). The p-value for the two-sided alternative hypothesis ($\beta_1 \ne 0$) is incredibly small, so we reject $H_0$. The data provide convincing evidence that height and weight are positively correlated. The true slope parameter is indeed greater than 0. (d) $R^2 = 0.72^2 = 0.52$. Approximately 52% of the variability in weight can be explained by the height of individuals.
(a) Roughly 0.53 to 0.67. (b) For individuals with one cm larger shoulder girth, their average height is predicted to be between 0.53 and 0.67 cm taller, with 98% confidence.
(a) Approximately 0.025. (b) $b_1 \pm 2.33 \times SE \rightarrow (0.546, 0.662).$ (c) For individuals with one cm larger shoulder girth, their average height is predicted to be between 0.546 and 0.662 cm taller, with 98% confidence.
(a) $r = \sqrt{0.518} \approx +0.72$. We know the correlation is positive due to the positive association between the variables seen in the scatterplot (above in previous exercise). (b) The residuals have a larger spread above the horizontal line at zero than below the line at zero. This indicates that the values are not symmetric around zero (so therefore not normally distributed). However, the violation is not extreme, and a simple least squares fit is probably appropriate for these data.
(a) $H_0: \beta_1 = 0$, $H_A: \beta_1 \ne 0$. (b) The observed slope of 2.559 is not a plausible value, the p-value is extremely small, and the null hypothesis can be rejected. (c) The p-value is also extremely small.
(a) Rough 90% confidence interval is 1.9 to 3.1. (b) For a one unit (one percentage point) increase in poverty across given metropolitan areas, the predicted average annual murder rate will be between 1.9 and 3.1 persons per million larger, with 90% confidence.
(a) $r = \sqrt{0.706} \approx +0.84$. We know the correlation is positive due to the positive association shown in the scatterplot. (b) The technical conditions all seem to be met.
(a) With only sixteen observations in the analysis there are not enough data points to establish any patterns in the residual plot. That said, the sixteen observations do not show any large deviations of LNE conditions. We do not know if the volunteers were friends, for example, which would violate the independence condition. (b) The layout of the points does not indicate any deviation form the LINE technical conditions. The small number of points, however, suggests that care should be given to making sure that the individuals in the study are a good representative sample of the population to which we would like to infer the results.
(a) The Linearity and Normality conditions seem to be met. If anything, the Equal variance condition is violated due to the a fan shaped pattern in the plot, which indicates non-constant variability in the residuals (little variability when $x$ is small, more variability when $x$ is large). We do not know if the cats were randomly sampled (i.e., are independent from one another), but we have no reason to believe that they are not independent. (b) Unequal variability does not affect the fit of the line. The line will continue to model the average heart weight of cats at a given body weight. However, the p-value for the inference on the line will be affected by the unequal variability. How much? Probably not much given that the violation is quite minimal.

A.25 Chapter 25

(a) (-0.044, 0.346). We are 95% confident that student who go out more than two nights a week on average have GPAs 0.044 points lower to 0.346 points higher than those who do not go out more than two nights a week, when controlling for the other variables in the model. (b) Yes, since the p-value is larger than 0.05 in all cases (not including the intercept).
(a) volume and diam; volume and height; diam and height. (b) Each is discernible in its own model. (c) When both diameter and height are used in the multiple linear regression model, both continue to be discernible predictors of volume.
(a) Linearity: Horror movies seem to show a much different pattern than the other genres. While the residuals plots show a random scatter over years and in order of data collection, there is a clear pattern in residuals for various genres, which signals that this regression model is not appropriate for these data. Independent observations: The variability of the residuals is higher for data that comes later in the dataset. We don’t know if the data are sorted by year, but if so, there may be a temporal pattern in the data that voilates the independence condition. Normality: The residuals are right skewed (skewed to the high end). Constant or Equal variability: The residuals vs. predicted values plot reveals some outliers. This plot for only babies with predicted birth weights between 6 and 8.5 pounds looks a lot better, suggesting that for bulk of the data the constant variance condition is met.
(a) Linearity: With so many observations in the dataset, we look for particularly extreme outliers in the histogram of residuals and do not see any. We also don’t see a non-linear pattern emerging in the residuals vs. predicted plot. Independent observations: The sample is random and there does not seem to be a trend in the residuals vs. order of data collection plot. Normality: The histogram of residuals appears to be unimodal and symmetic, centered at 0. Constant or equal variability: The residuals vs. predicted values plot reveals some outliers. This plot for only babies with predicted birth weights between 6 and 8.5 pounds looks a lot better, suggesting that for bulk of the data the constant variance condition is met. All concerns raised here are relatively mild. There are some outliers, but there is so much data that the influence of such observations will be minor. (b) $H_0$: The true slope coefficient of habit is zero ($\beta_5 = 0$). $H_A$: The true slope coefficient of height is different than zero ($\beta_5 \neq 0$). The p-value for the two-sided alternative hypothesis ($\beta_5 \ne 0$) is incredibly 0.0007 (smaller than 0.05), so we reject $H_0$. The data provide convincing evidence that height and weight are positively correlated, given the other variables in the model. The true slope parameter is indeed greater than 0.
(a) Roughly $\widehat{\texttt{weight}} = 11$ pounds and $\texttt{weight}_i = 7$ pounds. (b) Folds 1, 2, and 4 were used to build the prediction model. (c) The plot on the top estimates 8 parameters; the plot on the bottom estimates 3 parameters. (d) The residuals are not substantially different.
(a) The plots are difficult to differentiate. (b) The CV SSE is smaller for the model with only two predictors. (c) The model with more predictors seems to be over-fitting the data used to model build at the expense of not fitting (as well) the cross-validation hold out set for prediction.

A.26 Chapter 26

No, logistic regression is not appropriate because the response (or outcome) variable is not binary. Linear regression is likely to be more appropriate.
$H_0: \beta_1 = 0$, the slope of the model predicting kids’ marijuana use in college from their parents’ marijuana use in college is 0. $H_A: \beta_1 \neq 0$, the slope of the model predicting kids’ marijuana use in college from their parents’ marijuana use in college is different than 0. The test statistic is $Z = 4.09$ and the associated p-value is less than 0.0001. With a small p-value we reject $H_0$. The data provide convincing evidence that the slope of the model predicting kids’ marijuana use in college from their parents’ marijuana use in college is different than 0, i.e., that parents’ marijuana use in college is a discernible predictor of kids’ marijuana use in college.
(a) 26 observations are in Fold2. 8 correctly and 2 incorrectly predicted to be from Victoria. (b) 78 observations are used to build the model. (c) 2 coefficients for tail length; 3 coefficients for total length and sex.
(a) 76, 73.1%. (b) 58, 55.8%. (c) The tail length model should be chosen for classification purposes. (d) A model using all three predictors might be superior to either of the smaller models.