2  Study design

Before digging into the details of working with data, we stop to think about how data come to be. That is, if the data are to be used to make broad and complete conclusions, then it is important to understand who or what the data represent. One important aspect of data provenance is sampling. Knowing how the observational units were selected from a larger entity will allow for generalizations back to the population from which the data were randomly selected. Additionally, by understanding the structure of the study, causal relationships can be separated from those relationships which are only associated. A good question to ask oneself before working with the data at all is, “How were these observations collected?”. You will learn a lot about the data by understanding its source.

2.1 Sampling principles and strategies

The first step in conducting research is to identify topics or questions that are to be investigated. A clearly laid out research question is helpful in identifying what subjects or cases should be studied and what variables are important. It is also important to consider how data are collected so that the data are reliable and help achieve the research goals.

2.1.1 Populations and samples

Consider the following three research questions:

  1. What is the average mercury content in swordfish in the Atlantic Ocean?
  2. Over the last five years, what is the average time to complete a degree for Duke undergrads?
  3. Does a new drug reduce the number of deaths in patients with severe heart disease?

Each research question refers to a target population. In the first question, the target population is all swordfish in the Atlantic Ocean, and each fish represents a case. Oftentimes, it is not feasible to collect data for every case in a population. Collecting data for an entire population is called a census. A census is difficult because it is too expensive to collect data for the entire population, but it might also be because it is difficult or impossible to identify the entire population of interest! Instead, a sample is taken. A sample is the data you have. Ideally, a sample is a small fraction of the population. For instance, 60 swordfish (or some other number) in the population might be selected, and this sample data may be used to provide an estimate of the population average and to answer the research question.

For the second and third questions above, identify the target population and what represents an individual case.1

2.1.2 Parameters and statistics

In most statistical analysis procedures, the research question at hand boils down to understanding a numerical summary. The number (or set of numbers) may be a quantity you are already familiar with (like the average) or it may be something you learn through this text (like the slope and intercept from a least squares model, provided in Section 7.2).

A numerical summary can be calculated on either the sample of observations or the entire population. However, measuring every unit in the population is usually prohibitive. So, a “typical” numerical summary is calculated from a sample. Yet, we can still conceptualize calculating the average income of all adults in Argentina.

We use specific terms in order to differentiate when a number is being calculated on a sample of data (sample statistic) and when it is being calculated or considered for calculation on the entire population (population parameter). The terms statistic and parameter are useful for communicating claims and models and will be used extensively in later chapters which delve into making inference on populations.

2.1.3 Anecdotal evidence

Consider the following possible responses to the three research questions:

  1. A man on the news got mercury poisoning from eating swordfish, so the average mercury concentration in swordfish must be dangerously high.
  2. I met two students who took more than 7 years to graduate from Duke, so it must take longer to graduate at Duke than at many other colleges.
  3. My friend’s dad had a heart attack and died after they gave him a new heart disease drug, so the drug must not work.

Each conclusion is based on data. However, there are two problems. First, the data only represent one or two cases. Second, and more importantly, it is unclear whether these cases are actually representative of the population. Data collected in this haphazard fashion are called anecdotal evidence.

Anecdotal evidence.

Be careful of data collected in a haphazard fashion. Such evidence may be true and verifiable, but it may only represent extraordinary cases and therefore not be a good representation of the population.

Anecdotal evidence typically is composed of unusual cases that we recall based on their striking characteristics. For instance, we are more likely to remember the two people we met who took 7 years to graduate than the six others who graduated in four years. Instead, of looking at the most unusual cases, we should examine a sample of many cases that better represent the population.

2.1.4 Sampling from a population

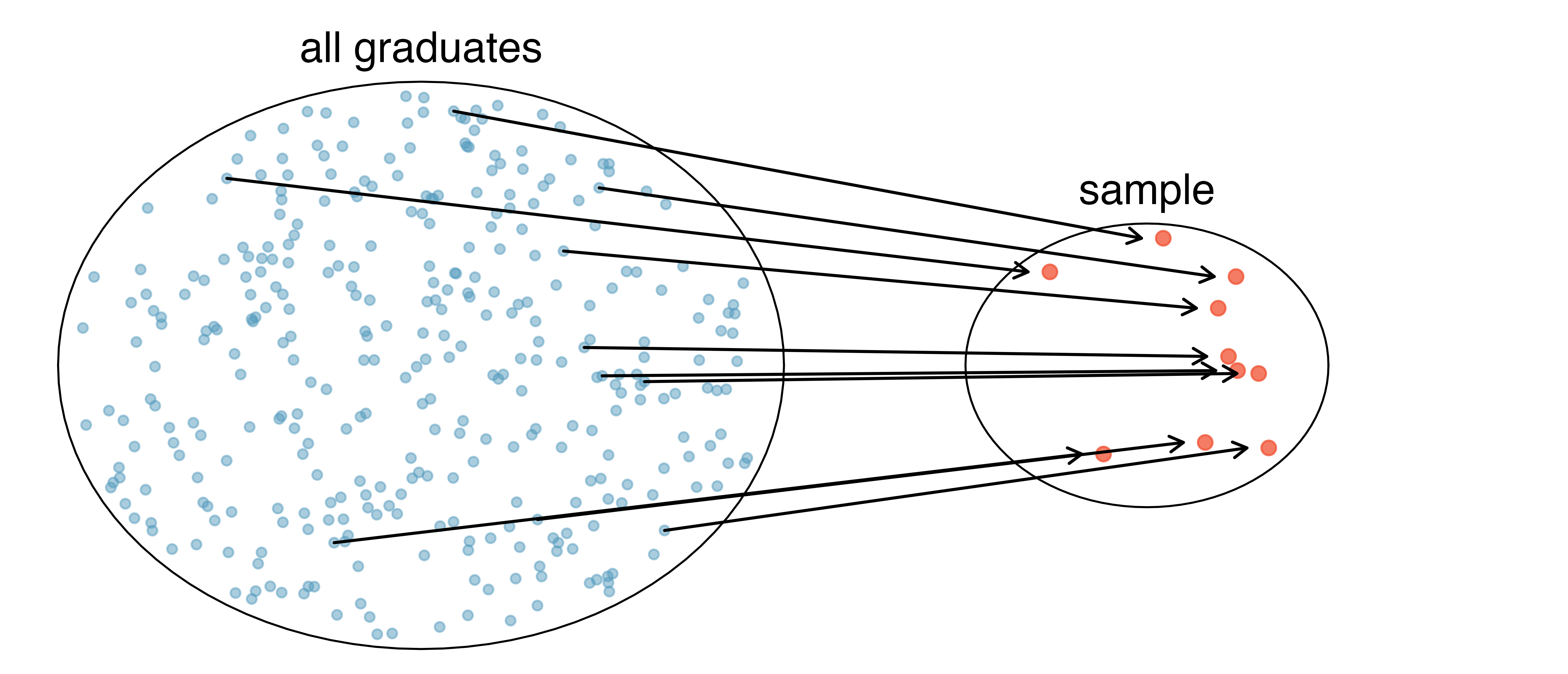
We might try to estimate the time to graduation for Duke undergraduates in the last five years by collecting a sample of graduates. All graduates in the last five years represent the population, and graduates who are selected for review are collectively called the sample. In general, we always seek to randomly select a sample from a population. The most basic type of random selection is equivalent to how raffles are conducted. For example, in selecting graduates, we could write each graduate’s name on a raffle ticket and draw 10 tickets. The selected names would represent a random sample of 10 graduates.

A large circle contains many dots which indicate all the graduates. A smaller circle contains a few of the dots (i.e., graduates) which have been randomly selected from the larger circle.
Figure 2.1: 10 graduates are randomly selected from the population to be included in the sample.

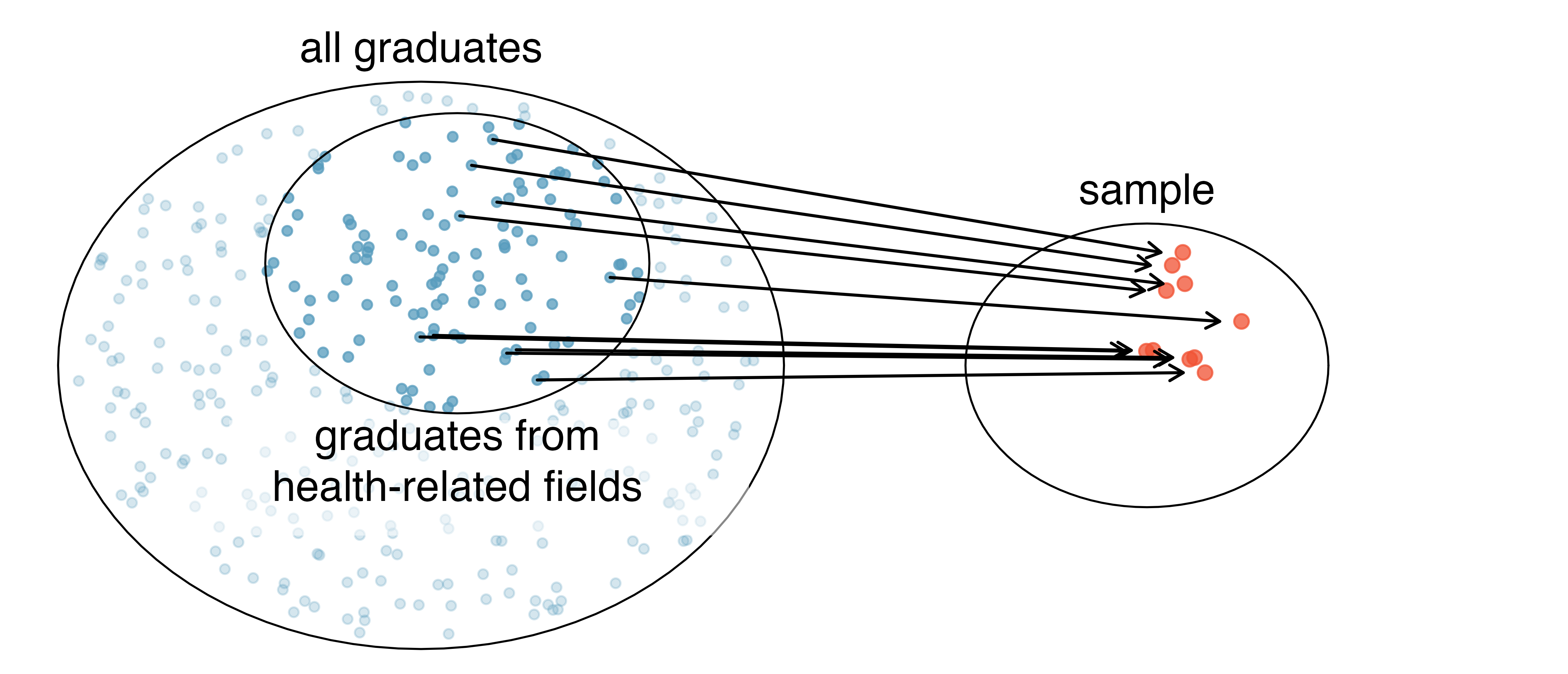
Suppose we ask a student who happens to be majoring in nutrition to select several graduates for the study. Which students do you think they might pick? Do you think their sample would be representative of all graduates?

They might pick a disproportionate number of graduates from health-related fields, as shown in Figure 2.2. When selecting samples by hand, we run the risk of picking a biased sample, even if our bias is unintended.

A large circle contains many dots which indicate all the graduates, but some of the dots have been greyed out where others are dark dots from which the sample is taken. A smaller circle contains a few of the dots (i.e., graduates) which have been selected from the biased group of dark dots in the large circle.
Figure 2.2: Asked to pick a sample of graduates, a nutrition major might inadvertently pick a disproportionate number of graduates from health-related majors.

If someone was permitted to pick and choose exactly which graduates were included in the sample, it is entirely possible that the sample would overrepresent that person’s interests, which may be entirely unintentional. This introduces bias into a sample. Sampling randomly helps address this problem. The most basic random sample is called a simple random sample and is equivalent to drawing names out of a hat to select cases. This means that each case in the population has an equal chance of being included and the cases in the sample are not related to each other.

The act of taking a simple random sample helps minimize bias. However, bias can crop up in other ways. Even when people are picked at random, e.g., for surveys, caution must be exercised if the non-response rate is high. For instance, if only 30% of the people randomly sampled for a survey actually respond, then it is unclear whether the results are representative of the entire population. This non-response bias can skew results.

A large circle contains many dots which indicate the population of interest, but some of the dots have been greyed out where others are dark dots from which the sample is taken (where the grey dots are potentially due to non-response bias). A smaller circle contains a few of the dots which have been selected from the group of dark dots in the large circle who were individuals willing to respond to the survey.
Figure 2.3: Due to the possibility of non-response, survey studies may only reach a certain group within the population. It is difficult, and oftentimes impossible, to completely fix this problem.

Another common downfall is a convenience sample, where individuals who are easily accessible are more likely to be included in the sample. For instance, if a political survey is done by stopping people walking in the Bronx, this will not represent all of New York City. It is often difficult to discern what sub-population a convenience sample represents.

We can easily access ratings for products, sellers, and companies through websites. These ratings are based only on those people who go out of their way to provide a rating. If 50% of online reviews for a product are negative, do you think this means that 50% of buyers are dissatisfied with the product? Why?2

2.1.5 Four sampling methods

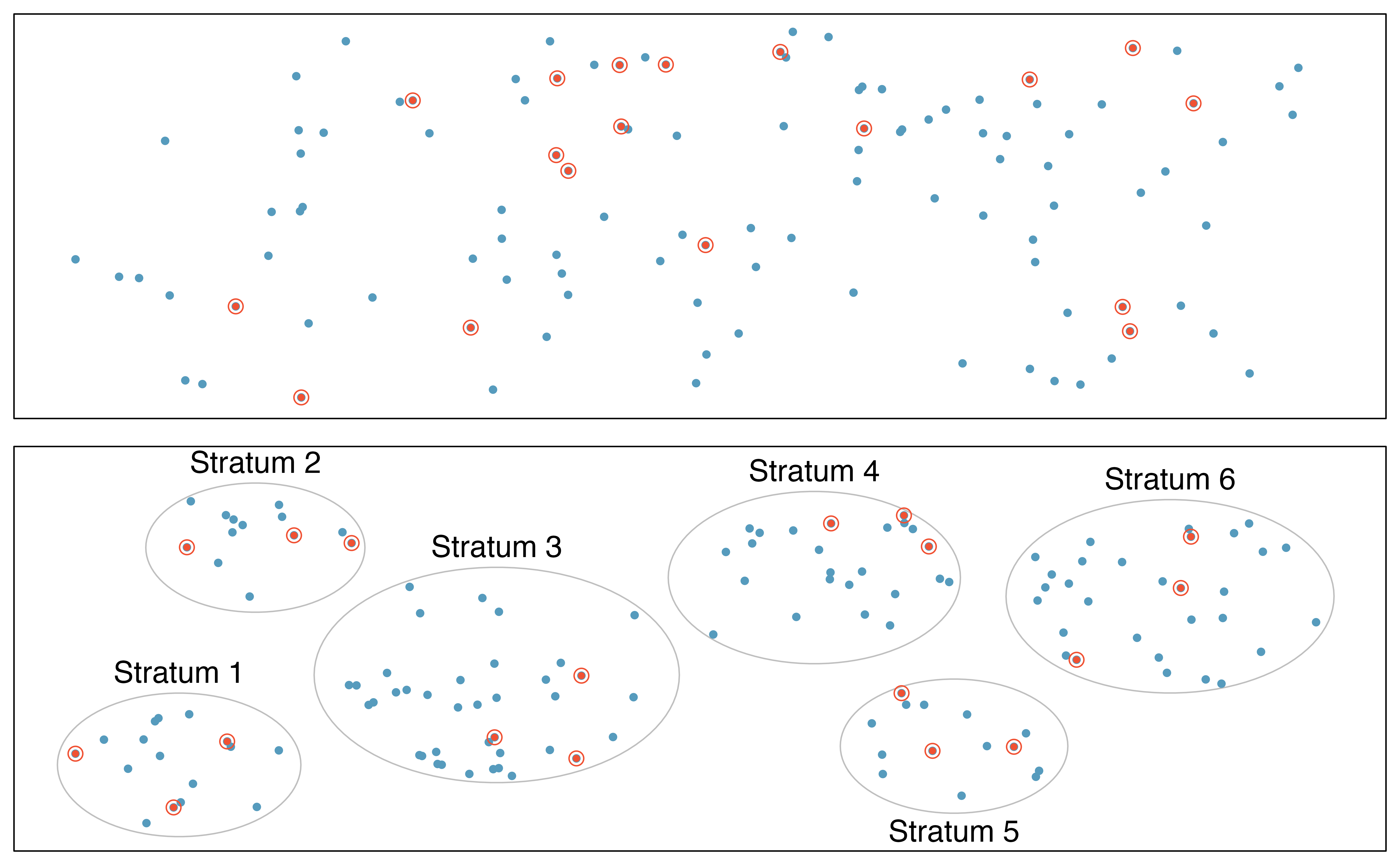
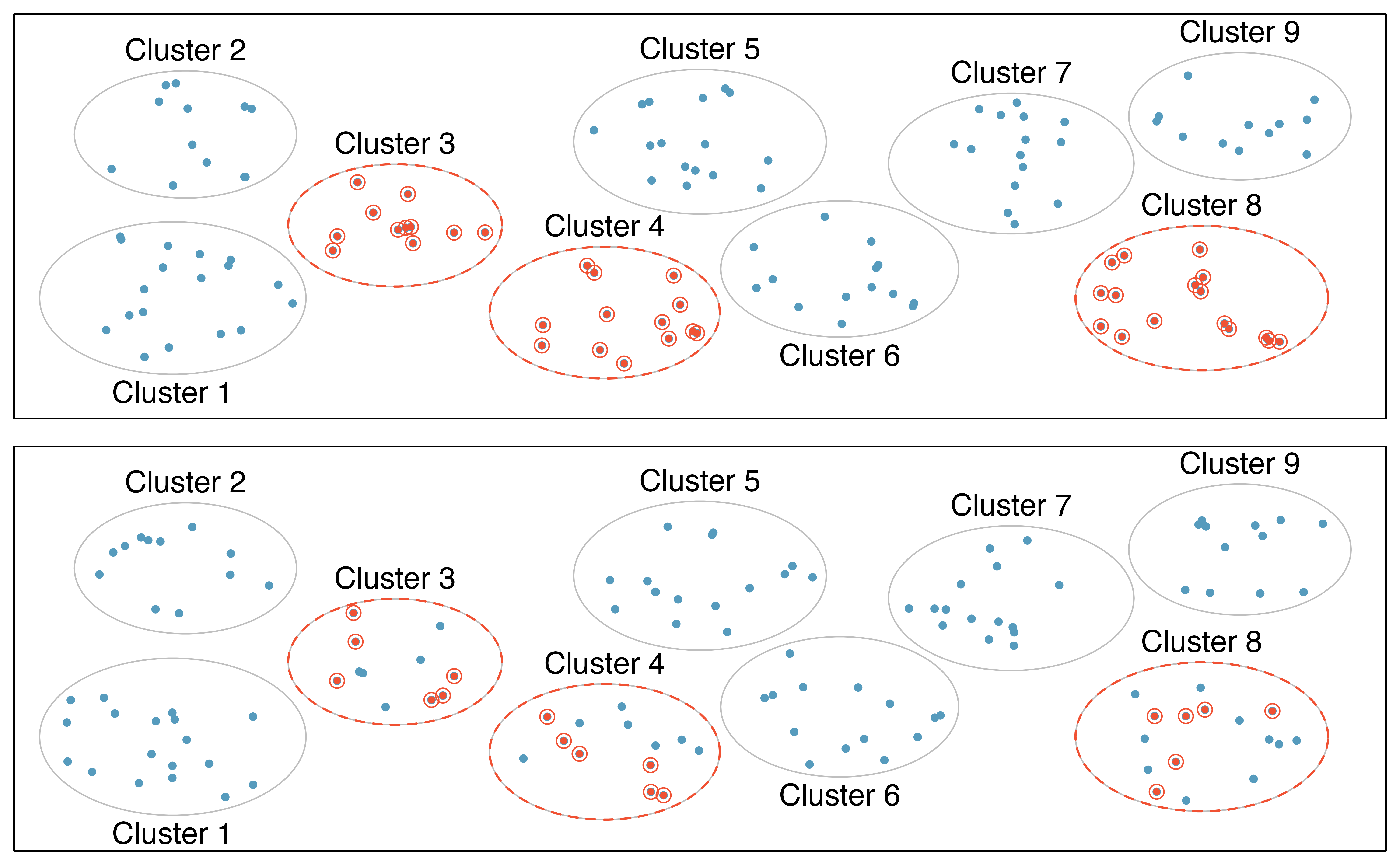
Almost all statistical methods are based on the notion of implied randomness. If data are not collected in a random framework from a population, these statistical methods – the estimates and errors associated with the estimates – are not reliable. Here we consider four random sampling techniques: simple, stratified, cluster, and multistage sampling. Figure 2.4 and Figure 2.5 provide graphical representations of these techniques.

Simple random sampling is probably the most intuitive form of random sampling. Consider the salaries of Major League Baseball (MLB) players, where each player is a member of one of the league’s 30 teams. To take a simple random sample of 120 baseball players and their salaries, we could write the names of that season’s several hundreds of players onto slips of paper, drop the slips into a bucket, shake the bucket around until we are sure the names are all mixed up, then draw out slips until we have the sample of 120 players. In general, a sample is referred to as “simple random” if each case in the population has an equal chance of being included in the final sample and knowing that a case is included in a sample does not provide useful information about which other cases are included.

The top box shows a population of dots (i.e., individuals) where a handful of the dots have been sampled randomly. The bottom box shows the same population of dots but grouped in such a way that there are six strata. From each stratum three dots (i.e., individuals) are randomly selected.
Figure 2.4: Examples of simple random and stratified sampling. In the top panel, simple random sampling was used to randomly select the 18 cases (denoted in red). In the bottom panel, stratified sampling was used: cases were first grouped into strata, then simple random sampling was employed to randomly select 3 cases within each stratum.’

Stratified sampling is a divide-and-conquer sampling strategy. The population is divided into groups called strata. The strata are chosen so that similar cases are grouped together, then a second sampling method, usually simple random sampling, is employed within each stratum. In the baseball salary example, each of the 30 teams could represent a stratum, since some teams have a lot more money (up to 4 times as much!). Then we might randomly sample 4 players from each team for our sample of 120 players.

Stratified sampling is especially useful when the cases in each stratum are very similar with respect to the outcome of interest. The downside is that analyzing data from a stratified sample is a more complex task than analyzing data from a simple random sample. The analysis methods introduced in this book would need to be extended to analyze data collected using stratified sampling.

Why would it be good for cases within each stratum to be very similar?

We might get a more stable estimate for the subpopulation in a stratum if the cases are very similar, leading to more precise estimates within each group. When we combine these estimates into a single estimate for the full population, that population estimate will tend to be more precise since each individual group estimate is itself more precise.

In a cluster sample, we break up the population into many groups, called clusters. Then we sample a fixed number of clusters and include all observations from each of those clusters in the sample. A multistage sample is like a cluster sample, but rather than keeping all observations in each cluster, we would collect a random sample within each selected cluster.

In the top figure, dots are grouped into clusters, three clusters are selected, and every dot (i.e., all individuals) from each of the three clusters are sampled. In the bottom figure, dots are again grouped into clusters and three clusters are selected. However, random sampling is applied so that a random sample from each of the three selected clusters is taken.
Figure 2.5: Examples of cluster and multistage sampling. In the top panel, cluster sampling was used: data were binned into nine clusters, three of these clusters were sampled, and all observations within these three clusters were included in the sample. In the bottom panel, multistage sampling was used, which differs from cluster sampling only in that we randomly select a subset of each cluster to be included in the sample rather than measuring every case in each sampled cluster.’

Sometimes cluster or multistage sampling can be more economical than the alternative sampling techniques. Also, unlike stratified sampling, these approaches are most helpful when there is a lot of case-to-case variability within a cluster but the clusters themselves do not look very different from one another. For example, if neighborhoods represented clusters, then cluster or multistage sampling work best when the populations inside each neighborhood are very diverse. A downside of these methods is that more advanced techniques are typically required to analyze the data, though the methods in this book can be extended to handle such data.

Suppose we are interested in estimating the malaria rate in a densely tropical portion of rural Indonesia. We learn that there are 30 villages in that part of the Indonesian jungle, each more or less like the next, but the distances between the villages are substantial. We want to test 150 individuals for malaria. What sampling method should we use?

A simple random sample would likely draw individuals from all 30 villages, which could make data collection expensive. Stratified sampling would be a challenge since it is unclear how we would build strata of similar individuals. However, cluster sampling or multistage sampling seem like very good ideas. With multistage sampling, we could randomly select half of the villages, then randomly select 10 people from each. This could reduce data collection costs substantially in comparison to a simple random sample, and the cluster sample would still yield reliable information, even if we would need to analyze the data with more advanced methods than those introduced in this book.

2.2 Experiments

Studies where the researchers assign treatments to cases are called experiments. When this assignment includes randomization, e.g., using a coin flip to decide which treatment a patient receives, it is called a randomized experiment. Randomized experiments are fundamentally important when trying to show a causal connection between two variables.

2.2.1 Principles of experimental design

  1. Controlling. Researchers assign treatments to cases, and they do their best to control any other differences in the groups3. For example, when patients take a drug in pill form, some patients take the pill with only a sip of water while others may have it with an entire glass of water. To control for the effect of water consumption, a doctor may instruct every patient to drink a 12-ounce glass of water with the pill.
  1. Randomization. Researchers randomize patients into treatment groups to account for variables that cannot be controlled. For example, some patients may be more susceptible to a disease than others due to their dietary habits. In this example dietary habit is a confounding variable4, which is defined as a variable that is associated with both the explanatory and response variables. Randomizing patients into the treatment or control group helps even out such differences.

Confounding variable.

A confounding variable is one that is associated with both the explanatory and response variables. Because it is associated with both variables, it prevents the study from concluding that the explanatory variable caused the response variable. Consider a silly example with total ice-cream sales as the explanatory variable and number of boating accidents as the response variable (which may seem highly correlated). Outside temperature is associated with both variables, and therefore we cannot conclude that high ice-cream sales is a cause of more boating accidents.

Confounding variables may or may not be measured as part of the study. Regardless, drawing cause-and-effect conclusions is difficult in an observational study because of the ever-present possibility of confounding variables.

  1. Replication. The more cases researchers observe, the more accurately they can estimate the effect of the explanatory variable on the response. In a single study, we replicate by collecting a sufficiently large sample. What is considered sufficiently large varies from experiment to experiment, but at a minimum we want to have multiple subjects (experimental units) per treatment group. Another way of achieving replication is replicating an entire study to verify an earlier finding. The term replication crisis refers to the ongoing methodological crisis in which past findings from scientific studies in several disciplines have failed to be replicated. Pseudoreplication occurs when individual observations under different treatments are heavily dependent on each other. For example, suppose you have 50 subjects in an experiment where you’re taking blood pressure measurements at 10 time points throughout the course of the study. By the end, you will have 50 \(\times\) 10 = 500 measurements. Reporting that you have 500 observations would be considered pseudoreplication, as the blood pressure measurements of a given individual are not independent of each other. Pseudoreplication often happens when the wrong entity is replicated, and the reported sample sizes are exaggerated.

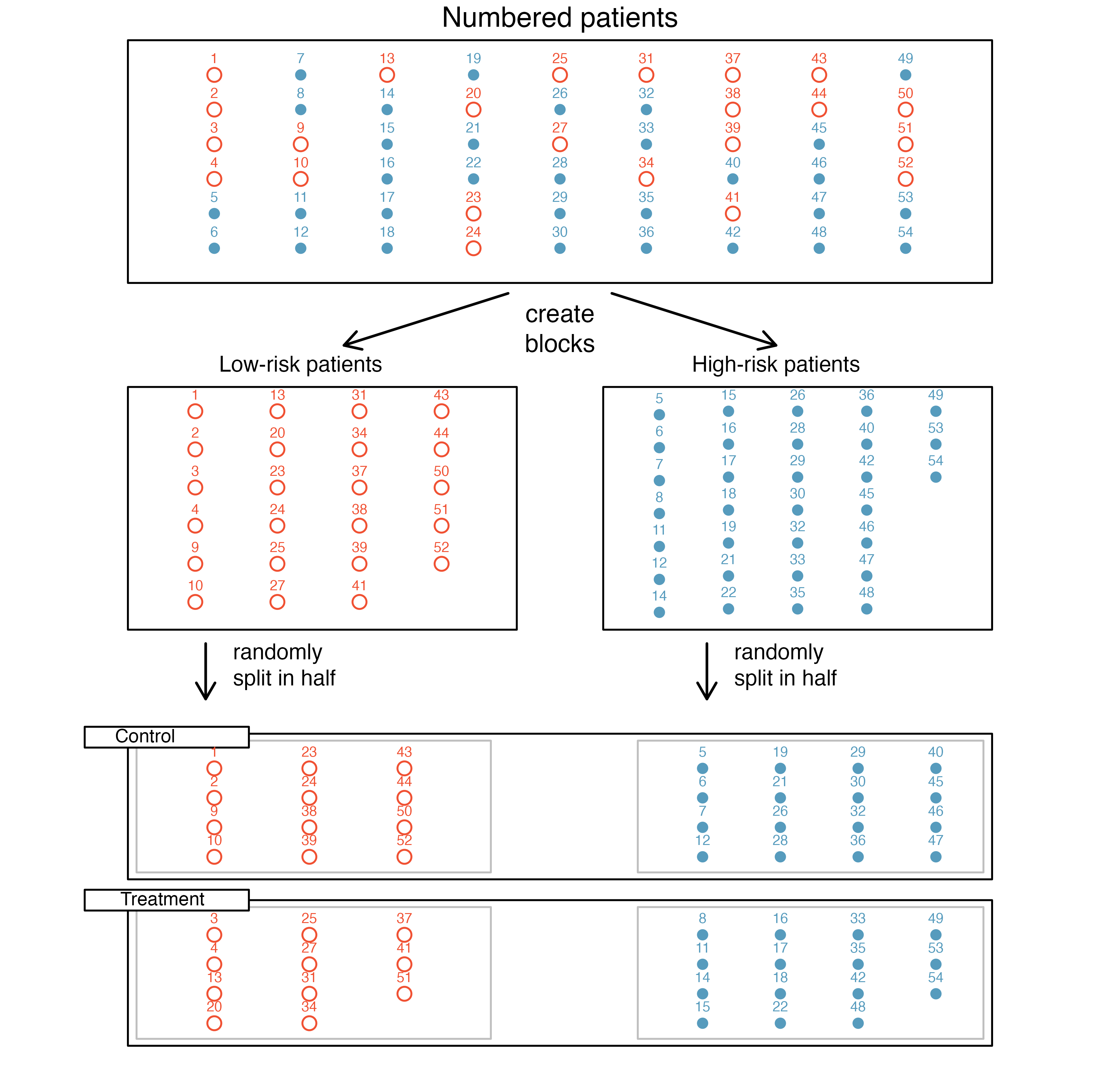
  1. Blocking. Researchers sometimes know or suspect that variables, other than the treatment, influence the response. Under these circumstances, they may first group individuals based on this variable into blocks and then randomize cases within each block to the treatment groups. This strategy is often referred to as blocking. For instance, if we are looking at the effect of a drug on heart attacks, we might first split patients in the study into low-risk and high-risk blocks, then randomly assign half the patients from each block to the control group and the other half to the treatment group, as shown in Figure 2.6. This strategy ensures that each treatment group has the same number of low-risk patients and the same number of high-risk patients.
Before randomly allocating, the red low risk patients and blue high risk patients are split into two separate groups. Subsequently, half of the red low risk patients are randomly chosen to receive the treatment, and half of the blue high risk patients are randomly chosen to receive the treatment.
Figure 2.6: Blocking for patient risk. Patients are first divided into low-risk and high-risk blocks, then patients in each block are evenly randomized into the treatment groups. This strategy ensures equal representation of patients in each treatment group from both risk categories.

It is important to incorporate the first three experimental design principles into any study, and this book describes applicable methods for analyzing data from such experiments. Blocking is a slightly more advanced technique, and statistical methods in this book may be extended to analyze data collected using blocking.

2.2.2 Reducing bias in human experiments

Randomized experiments have long been considered to be the gold standard for data collection, but they do not ensure an unbiased perspective into the cause-and-effect relationship in all cases. Human studies are perfect examples where bias can unintentionally arise. Here we reconsider a study where a new drug was used to treat heart attack patients. In particular, researchers wanted to know if the drug reduced deaths in patients.

These researchers designed a randomized experiment because they wanted to draw causal conclusions about the drug’s effect. Study volunteers5 were randomly placed into two study groups. One group, the treatment group, received the drug. The other group, called the control group, did not receive any drug treatment.

Put yourself in the place of a person in the study. If you are in the treatment group, you are given a fancy new drug that you anticipate will help you. On the other hand, a person in the other group does not receive the drug and sits idly, hoping her participation does not increase her risk of death. These perspectives suggest there are actually two effects in this study: the one of interest is the effectiveness of the drug, and the second is an emotional effect of (not) taking the drug, which is difficult to quantify.

Researchers aren’t usually interested in the emotional effect, which might bias the study. To circumvent this problem, researchers do not want patients to know which group they are in. When researchers keep the patients uninformed about their treatment, the study is said to be blind. But there is one problem: if a patient does not receive a treatment, they will know they’re in the control group. A solution to this problem is to give a fake treatment to patients in the control group. This is called a placebo, and an effective placebo is the key to making a study truly blind. A classic example of a placebo is a sugar pill that is made to look like the actual treatment pill. However, offering such a fake treatment may not be ethical in certain experiments. For example, in medical experiments, typically the control group must get the current standard of care. Oftentimes, a placebo results in a slight but real improvement in patients. This effect has been dubbed the placebo effect.

The patients are not the only ones who should be blinded: doctors and researchers can unintentionally bias a study. When a doctor knows a patient has been given the real treatment, they might inadvertently give that patient more attention or care than a patient that they know is on the placebo. To guard against this bias, which again has been found to have a measurable effect in some instances, most modern studies employ a double-blind setup where doctors or researchers who interact with patients are, just like the patients, unaware of who is or is not receiving the treatment.6

Look back to the study in Section 1.1 where researchers were testing whether stents were effective at reducing strokes in at-risk patients. Is this an experiment? Was the study blinded? Was it double-blinded?7

For the study in Section 1.1, could the researchers have employed a placebo? If so, what would that placebo have looked like?8

You may have many questions about the ethics of sham surgeries to create a placebo. These questions may have even arisen in your mind when in the general experiment context, where a possibly helpful treatment was withheld from individuals in the control group; the main difference is that a sham surgery tends to create additional risk, while withholding a treatment only maintains a person’s risk.

There are always multiple viewpoints of experiments and placebos, and rarely is it obvious which is ethically “correct”. For instance, is it ethical to use a sham surgery when it creates a risk to the patient? However, if we do not use sham surgeries, we may promote the use of a costly treatment that has no real effect; if this happens, money and other resources will be diverted away from other treatments that are known to be helpful. Ultimately, this is a difficult situation where we cannot perfectly protect both the patients who have volunteered for the study and the patients who may benefit (or not) from the treatment in the future.

2.3 Observational studies

Studies where no treatment has been explicitly applied (or explicitly withheld) are called observational studies. For instance, studies on the loan data and county data described in Section 1.2 are would both be considered observational, as they rely on observational data.

Making causal conclusions based on experiments is often reasonable, since we can randomly assign the explanatory variable(s), i.e., the treatments. However, making the same causal conclusions based on observational data can be treacherous and is not recommended. Thus, observational studies are generally only sufficient to show associations or form hypotheses that can be later checked with experiments.

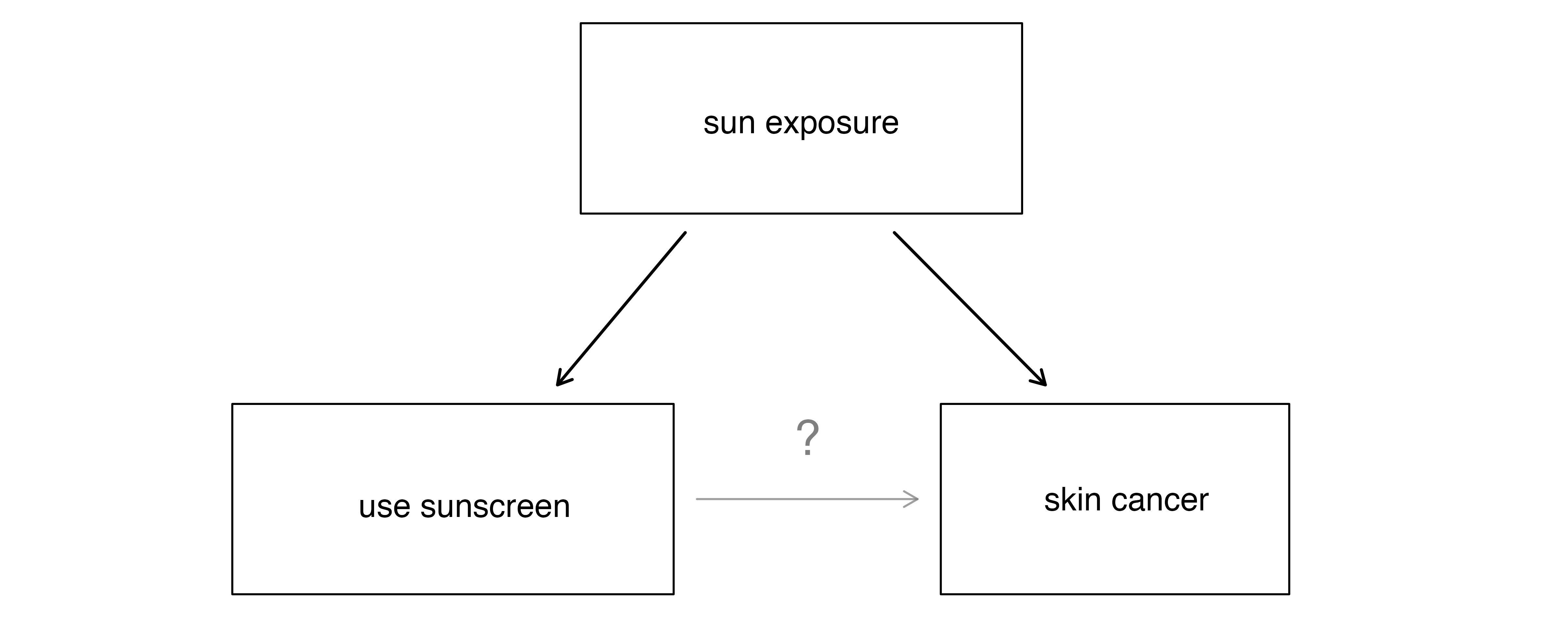
Suppose an observational study tracked sunscreen use and skin cancer, and it was found that the more sunscreen someone used, the more likely the person was to have skin cancer. Does this mean sunscreen causes skin cancer?

No! Some previous research tells us that using sunscreen actually reduces skin cancer risk, so maybe there is another variable that can explain this hypothetical association between sunscreen usage and skin cancer, as shown in Figure 2.7. One important piece of information that is absent is sun exposure. If someone is out in the sun all day, they are more likely to use sunscreen and more likely to get skin cancer. Exposure to the sun is unaccounted for in the simple observational investigation.

Three boxes are shown in a triangle arrangement representing: sun exposure, using sunscreen, and skin cancer. A solid arrow connects sun exposure as a causal mechanism to using sunscreen; a solid arrow also connects sun exposure as a causal mechanism to skin cancer. A questioning arrow indicates that the causal effect of using sunscreen on skin cancer is unknown.
Figure 2.7: Sun exposure may be the root cause of both sunscreen use and skin cancer.

In this example, sun exposure is a confounding variable. The presence of confounding variables is what inhibits the ability for observational studies to make causal claims. While one method to justify making causal conclusions from observational studies is to exhaust the search for confounding variables, there is no guarantee that all confounding variables can be examined or measured.

Figure 1.2 shows a negative association between the homeownership rate and the percentage of housing units that are in multi-unit structures in a county. However, it is unreasonable to conclude that there is a causal relationship between the two variables. Suggest a variable that might explain the negative relationship.9

Observational studies come in two forms: prospective and retrospective studies. A prospective study identifies individuals and collects information as events unfold. For instance, medical researchers may identify and follow a group of patients over many years to assess the possible influences of behavior on cancer risk. One example of such a study is The Nurses’ Health Study. Started in 1976 and expanded in 1989, the Nurses’ Health Study has collected data on over 275,000 nurses and is still enrolling participants. This prospective study recruits registered nurses and then collects data from them using questionnaires. Retrospective studies collect data after events have taken place, e.g., researchers may review past events in medical records. Some datasets may contain both prospectively- and retrospectively collected variables, such as medical studies which gather information on participants’ lives before they enter the study and subsequently collect data on participants throughout the study.

2.4 Chapter review

2.4.1 Summary

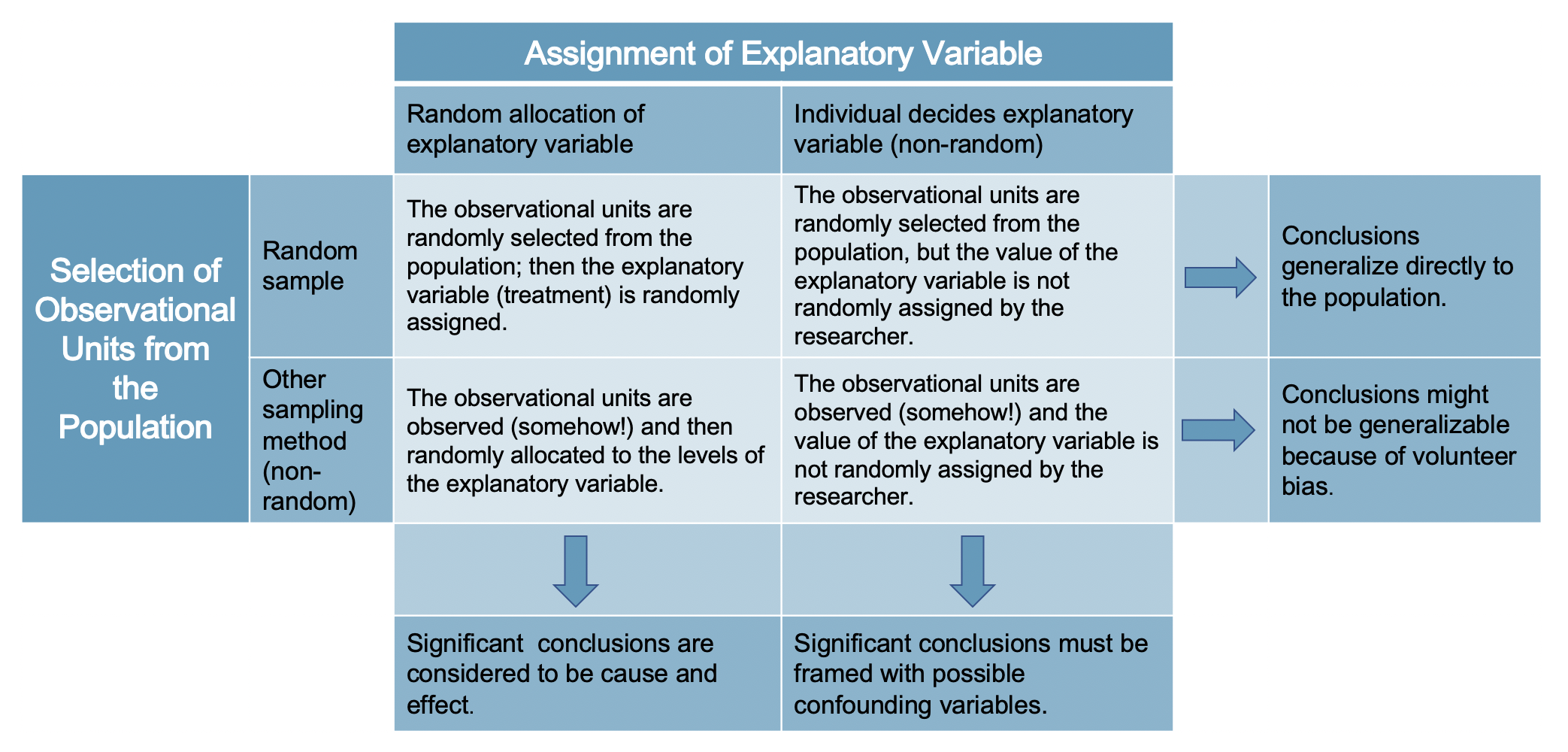
A proficient analyst will have a good sense of the types of data they are working with and how to visualize the data in order to gain a complete understanding of the variables. Equally important, however, is the data source. In this chapter, we have discussed randomized experiments and taking good, random, representative samples from a population. When we discuss inferential methods (starting in Chapter 11), the conclusions that can be drawn will be dependent on how the data were collected. Figure 2.8 summarizes how sampling and assignment methods relate to the scope of inference.10 Regularly revisiting Figure 2.8 will be important when making conclusions from a given data analysis.

A two by two table describing the scenarios of random sample or not and random allocation or not. Selecting randomly from a population allows for generalization back to the population. Randomly allocating in an experiment allows for establishing causation.
Figure 2.8: Analysis conclusions should be made carefully according to how the data were collected. Very few datasets come from the top left box because usually ethics require that random assignment of treatments can only be given to volunteers. Both representative (ideally random) sampling and experiments (random assignment of treatments) are important for how statistical conclusions can be made on populations.

2.4.2 Terms

The terms introduced in this chapter are presented in Table 2.1. If you’re not sure what some of these terms mean, we recommend you go back in the text and review their definitions. You should be able to easily spot them as bolded text.

Table 2.1: Terms introduced in this chapter.
anecdotal evidence experiment replication
bias multistage sample replication crisis
blind non-response bias representative
blocking non-response rate retrospective study
census observational study sample
cluster placebo sample bias
cluster sampling placebo effect sample statistic
confounding variable population simple random sample
control population parameter simple random sampling
control group prospective study strata
convenience sample pseudoreplication stratified sampling
double-blind randomized experiment treatment group

2.5 Exercises

Answers to odd-numbered exercises can be found in Appendix A.2.

  1. Parameters and statistics. Identify which value represents the sample mean and which value represents the claimed population mean.

    1. American households spent an average of about $52 in 2007 on Halloween merchandise such as costumes, decorations and candy. To see if this number had changed, researchers conducted a new survey in 2008 before industry numbers were reported. The survey included 1,500 households and found that average Halloween spending was $58 per household.

    2. The average GPA of students in 2001 at a private university was 3.37. A survey on a sample of 203 students from this university yielded an average GPA of 3.59 a decade later.

  1. Sleeping in college. A recent article in a college newspaper stated that college students get an average of 5.5 hrs of sleep each night. A student who was skeptical about this value decided to conduct a survey by randomly sampling 25 students. On average, the sampled students slept 6.25 hours per night. Identify which value represents the sample mean and which value represents the claimed population mean.

  1. Air pollution and birth outcomes, scope of inference. Researchers collected data to examine the relationship between air pollutants and preterm births in Southern California. During the study air pollution levels were measured by air quality monitoring stations. Length of gestation data were collected on 143,196 births between the years 1989 and 1993, and air pollution exposure during gestation was calculated for each birth. (Ritz et al. 2000)

    1. Identify the population of interest and the sample in this study.

    2. Comment on whether the results of the study can be generalized to the population, and if the findings of the study can be used to establish causal relationships.

  1. Cheaters, scope of inference. Researchers studying the relationship between honesty, age and self-control conducted an experiment on 160 children between the ages of 5 and 15. The researchers asked each child to toss a fair coin in private and to record the outcome (white or black) on a paper sheet, and said they would only reward children who report white. Half the students were explicitly told not to cheat and the others were not given any explicit instructions. Differences were observed in the cheating rates in the instruction and no instruction groups, as well as some differences across children’s characteristics within each group. (Bucciol and Piovesan 2011)

    1. Identify the population of interest and the sample in this study.

    2. Comment on whether the results of the study can be generalized to the population, and if the findings of the study can be used to establish causal relationships.

  1. Gamification and statistics, scope of inference. Researchers investigating the effects of gamification (application of game-design elements and game principles in non-game contexts) on learning statistics randomly assigned 365 college students in a statistics course to one of four groups; one of these groups had no reading exercises and no gamification, one group had reading but no gamification, one group had gamification but no reading, and a final group had gamification and reading. Students in all groups also attended lectures. The study found that gamification had a positive impact on student learning compared to traditional teaching methods involving reading exercises. (Legaki et al. 2020)

    1. Identify the population of interest and the sample in this study.

    2. Comment on whether the results of the study can be generalized to the population, and if the findings of the study can be used to establish causal relationships.

  1. Stealers, scope of inference. In a study of the relationship between socio-economic class and unethical behavior, 129 University of California undergraduates at Berkeley were asked to identify themselves as having low or high social-class by comparing themselves to others with the most (least) money, most (least) education, and most (least) respected jobs. They were also presented with a jar of individually wrapped candies and informed that the candies were for children in a nearby laboratory, but that they could take some if they wanted. After completing some unrelated tasks, participants reported the number of candies they had taken. It was found that those who were identified as upper-class took more candy than others. (Piff et al. 2012)

    1. Identify the population of interest and the sample in this study.

    2. Comment on whether the results of the study can be generalized to the population, and if the findings of the study can be used to establish causal relationships.

  1. Relaxing after work. The General Social Survey asked the question, “After an average work day, about how many hours do you have to relax or pursue activities that you enjoy?” to a random sample of 1,155 Americans. The average relaxing time was found to be 1.65 hours. Determine which of the following is an observation, a variable, a sample statistic, or a population parameter.11

    1. An American in the sample.

    2. Number of hours spent relaxing after an average work day.

    3. 1.65.

    4. Average number of hours all Americans spend relaxing after an average work day.

  1. Cats on YouTube. Suppose you want to estimate the percentage of videos on YouTube that are cat videos. It is impossible for you to watch all videos on YouTube so you use a random video picker to select 1000 videos for you. You find that 2% of these videos are cat videos. Determine which of the following is an observation, a variable, a sample statistic, or a population parameter.

    1. Percentage of all videos on YouTube that are cat videos.

    2. 2%.

    3. A video in your sample.

    4. whether a video is a cat video.

  1. Course satisfaction across sections. A large college class has 160 students. All 160 students attend the lectures together, but the students are divided into 4 groups, each of 40 students, for lab sections administered by different teaching assistants. The professor wants to conduct a survey about how satisfied the students are with the course, and he believes that the lab section a student is in might affect the student’s overall satisfaction with the course.

    1. What type of study is this?

    2. Suggest a sampling strategy for carrying out this study.

  1. Housing proposal across dorms. On a large college campus first-year students and sophomores live in dorms located on the eastern part of the campus and juniors and seniors live in dorms located on the western part of the campus. Suppose you want to collect student opinions on a new housing structure the college administration is proposing and you want to make sure your survey equally represents opinions from students from all years.

    1. What type of study is this?

    2. Suggest a sampling strategy for carrying out this study.

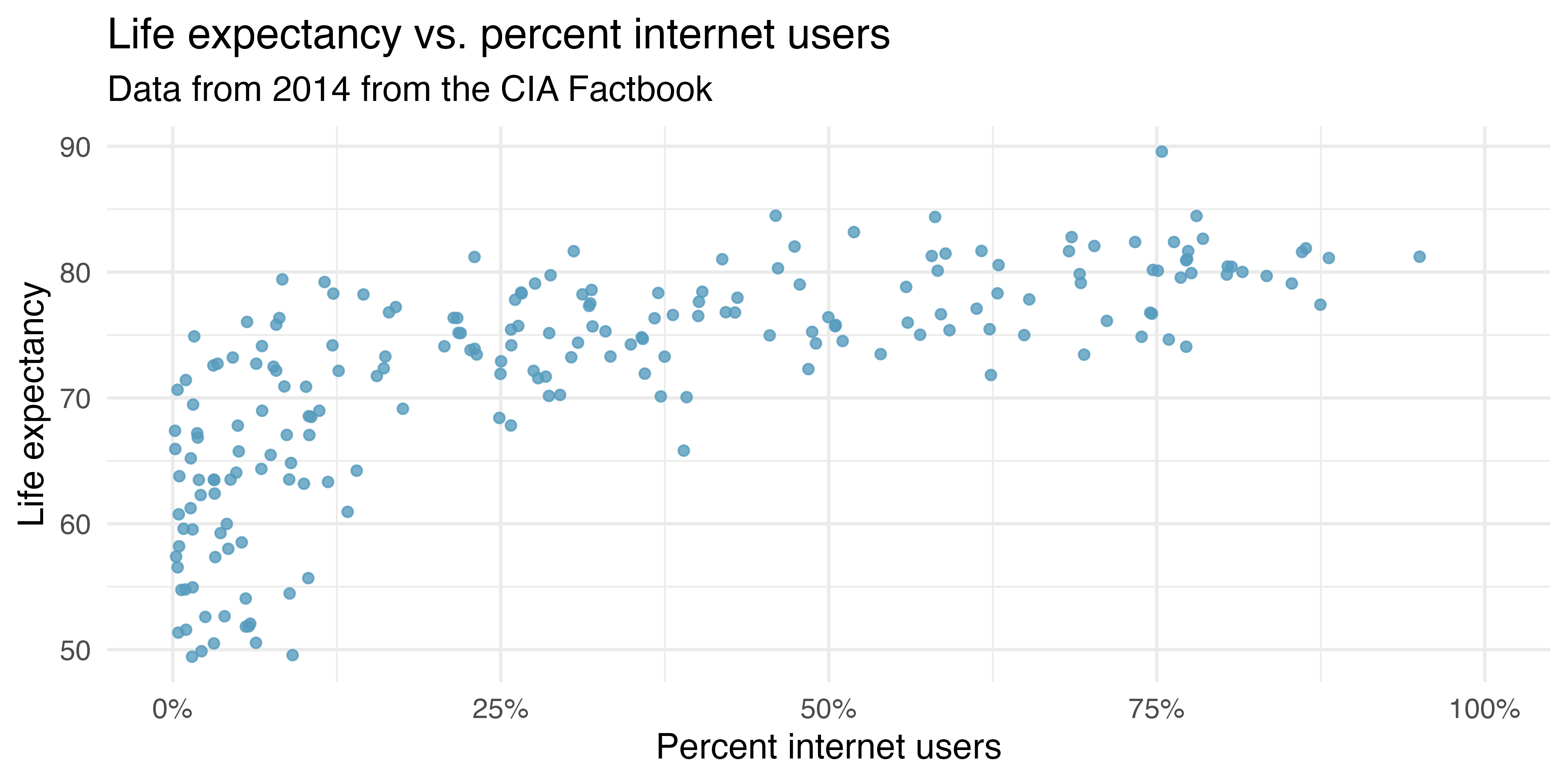
  1. Internet use and life expectancy. The following scatterplot was created as part of a study evaluating the relationship between estimated life expectancy at birth (as of 2014) and percentage of internet users (as of 2009) in 208 countries for which such data were available.12

    1. Describe the relationship between life expectancy and percentage of internet users.

    2. What type of study is this?

    3. State a possible confounding variable that might explain this relationship and describe its potential effect.

  1. Stressed out. A study that surveyed a random sample of otherwise healthy high school students found that they are more likely to get muscle cramps when they are stressed. The study also noted that students drink more coffee and sleep less when they are stressed.

    1. What type of study is this?

    2. Can this study be used to conclude a causal relationship between increased stress and muscle cramps?

    3. State possible confounding variables that might explain the observed relationship between increased stress and muscle cramps.

  1. Evaluate sampling methods. A university wants to determine what fraction of its undergraduate student body support a new $25 annual fee to improve the student union. For each proposed method below, indicate whether the method is reasonable or not.

    1. Survey a simple random sample of 500 students.

    2. Stratify students by their field of study, then sample 10% of students from each stratum.

    3. Cluster students by their ages (e.g., 18 years old in one cluster, 19 years old in one cluster, etc.), then randomly sample three clusters and survey all students in those clusters.

  1. Random digit dialing. The Gallup Poll uses a procedure called random digit dialing, which creates phone numbers based on a list of all area codes in America in conjunction with the associated number of residential households in each area code. Give a possible reason the Gallup Poll chooses to use random digit dialing instead of picking phone numbers from the phone book.

  1. Haters are gonna hate, study confirms. A study published in the Journal of Personality and Social Psychology asked a group of 200 randomly sampled participants recruited online using Amazon’s Mechanical Turk to evaluate how they felt about various subjects, such as camping, health care, architecture, taxidermy, crossword puzzles, and Japan in order to measure their attitude towards mostly independent stimuli. Then, they presented the participants with information about a new product: a microwave oven. This microwave oven does not exist, but the participants didn’t know this, and were given three positive and three negative fake reviews. People who reacted positively to the subjects on the dispositional attitude measurement also tended to react positively to the microwave oven, and those who reacted negatively tended to react negatively to it. Researchers concluded that “some people tend to like things, whereas others tend to dislike things, and a more thorough understanding of this tendency will lead to a more thorough understanding of the psychology of attitudes.” (Hepler and Albarracı́n 2013)

    1. What are the cases?

    2. What is (are) the response variable(s) in this study?

    3. What is (are) the explanatory variable(s) in this study?

    4. Does the study employ random sampling? Explain your reasoning.

    5. Is this an observational study or an experiment? Explain your reasoning.

    6. Can we establish a causal link between the explanatory and response variables?

    7. Can the results of the study be generalized to the population at large?

  1. Reading the paper. Below are excerpts from two articles published in the NY Times:

    1. An excerpt from an article titled Risks: Smokers Found More Prone to Dementia is below. Based on this study, can we conclude that smoking causes dementia later in life? Explain your reasoning. (Rabin 2010)

    “Researchers analyzed data from 23,123 health plan members who participated in a voluntary exam and health behavior survey from 1978 to 1985, when they were 50-60 years old. 23 years later, about 25% of the group had dementia, including 1,136 with Alzheimer’s disease and 416 with vascular dementia. After adjusting for other factors, the researchers concluded that pack-a-day smokers were 37% more likely than nonsmokers to develop dementia, and the risks went up with increased smoking; 44% for one to two packs a day; and twice the risk for more than two packs.”

    1. An excerpt from an article titled The School Bully Is Sleepy is below. A friend of yours who read the article says, “The study shows that sleep disorders lead to bullying in school children.” Is this statement justified? If not, how best can you describe the conclusion that can be drawn from this study? (Parker-Pope 2011)

    “The University of Michigan study, collected survey data from parents on each child’s sleep habits and asked both parents and teachers to assess behavioral concerns. About a third of the students studied were identified by parents or teachers as having problems with disruptive behavior or bullying. The researchers found that children who had behavioral issues and those who were identified as bullies were twice as likely to have shown symptoms of sleep disorders.”

  1. Sampling strategies. A statistics student who is curious about the relationship between the amount of time students spend on social networking sites and their performance at school decides to conduct a survey. Various research strategies for collecting data are described below. In each, name the sampling method proposed and any bias you might expect.

    1. They randomly sample 40 students from the study’s population, give them the survey, ask them to fill it out, and bring it back the next day.

    2. They give out the survey only to their friends, making sure each one of them fills it out.

    3. They post a link to an online survey on Facebook and ask their friends to fill it out.

    4. They randomly sample 5 classes and asks a random sample of students from those classes to fill out the survey.

  1. Family size. Suppose we want to estimate household size, where a “household” is defined as people living together in the same dwelling, and sharing living accommodations. If we select students at random at an elementary school and ask them what their family size is, will this be a good measure of household size? Or will our average be biased? If so, will it overestimate or underestimate the true value?

  1. Light and exam performance. A study is designed to test the effect of light level on exam performance of students. The researcher believes that light levels might have different effects on people who wear glasses and people who don’t, so they want to make sure both groups of people are equally represented in each treatment. The treatments are fluorescent overhead lighting, yellow overhead lighting, no overhead lighting (only desk lamps).

    1. What is the response variable?

    2. What is the explanatory variable? What are its levels?

    3. What is the blocking variable? What are its levels?

  1. Vitamin supplements. To assess the effectiveness of taking large doses of vitamin C in reducing the duration of the common cold, researchers recruited 400 healthy volunteers from staff and students at a university. A quarter of the patients were assigned a placebo, and the rest were evenly divided between 1g Vitamin C, 3g Vitamin C, or 3g Vitamin C plus additives to be taken at onset of a cold for the following two days. All tablets had identical appearance and packaging. The nurses who handed the prescribed pills to the patients knew which patient received which treatment, but the researchers assessing the patients when they were sick did not. No statistically discernible differences were observed in any measure of cold duration or severity between the four groups, and the placebo group had the shortest duration of symptoms. (Audera et al. 2001)

    1. Was this an experiment or an observational study? Why?

    2. What are the explanatory and response variables in this study?

    3. Were the patients blinded to their treatment?

    4. Was this study double-blind?

    5. Participants are ultimately able to choose whether to use the pills prescribed to them. We might expect that not all of them will adhere and take their pills. Does this introduce a confounding variable to the study? Explain your reasoning.

  1. Light, noise, and exam performance. A study is designed to test the effect of light level and noise level on exam performance of students. The researcher believes that light and noise levels might have different effects on people who wear glasses and people who don’t, so they want to make sure both groups of people are equally represented in each treatment. The light treatments considered are fluorescent overhead lighting, yellow overhead lighting, no overhead lighting (only desk lamps). The noise treatments considered are no noise, construction noise, and human chatter noise.

    1. What type of study is this?

    2. How many factors are considered in this study? Identify them, and describe their levels.

    3. What is the role of the wearing glasses variable in this study?

  1. Music and learning. You would like to conduct an experiment in class to see if students learn better if they study without any music, with music that has no lyrics (instrumental), or with music that has lyrics. Briefly outline a design for this study.
  1. Soda preference. You would like to conduct an experiment in class to see if your classmates prefer the taste of regular Coke or Diet Coke. Briefly outline a design for this study.

  1. Exercise and mental health. A researcher is interested in the effects of exercise on mental health and they propose the following study: use stratified random sampling to ensure representative proportions of 18-30, 31-40 and 41- 55 year-olds from the population. Next, randomly assign half the subjects from each age group to exercise twice a week, and instruct the rest not to exercise. Conduct a mental health exam at the beginning and at the end of the study, and compare the results.

    1. What type of study is this?

    2. What are the treatment and control groups in this study?

    3. Does this study make use of blocking? If so, what is the blocking variable?

    4. Does this study make use of blinding?

    5. Comment on whether the results of the study can be used to establish a causal relationship between exercise and mental health, and indicate whether the conclusions can be generalized to the population at large.

    6. Suppose you are given the task of determining if this proposed study should get funding. Would you have any reservations about the study proposal?

  1. Chia seeds and weight loss. Chia Pets – those terra-cotta figurines that sprout fuzzy green hair – made the chia plant a household name. But chia has since gained a reputation as a diet supplement. In one 2009 study, 38 men and 38 women were recruited and and divided each randomly into two groups: treatment or control. One group was given 25 grams of chia seeds twice a day, and the other was given a placebo. The subjects volunteered to be a part of the study. After 12 weeks, the scientists found no statistically discernible difference between the groups in appetite or weight loss. (Nieman et al. 2009)

    1. What type of study is this?

    2. What are the experimental and control treatments in this study?

    3. Has blocking been used in this study? If so, what is the blocking variable?

    4. Has blinding been used in this study?

    5. Comment on whether we can make a causal statement, and indicate whether we can generalize the conclusion to the population at large.

  1. City council survey. A city council has requested a household survey be conducted in a suburban area of their city. The area is broken into many distinct and unique neighborhoods, some including large homes, some with only apartments, and others a diverse mixture of housing structures. For each part below, identify the sampling methods described, and describe the statistical pros and cons of the method in the city’s context.

    1. Randomly sample 200 households from the city.

    2. Divide the city into 20 neighborhoods, and then sample 10 households from each neighborhood.

    3. Divide the city into 20 neighborhoods, randomly sample 3 neighborhoods, and then sample all households from those 3 neighborhoods.

    4. Divide the city into 20 neighborhoods, randomly sample 8 neighborhoods, and then randomly sample 50 households from those neighborhoods.

    5. Sample the 200 households closest to the city council offices.

  1. Flawed reasoning. Identify the flaw(s) in reasoning in the following scenarios. Explain what the individuals in the study should have done differently if they wanted to make such strong conclusions.

    1. Students at an elementary school are given a questionnaire that they are asked to return after their parents have completed it. One of the questions asked is, “Do you find that your work schedule makes it difficult for you to spend time with your kids after school?” Of the parents who replied, 85% said “no”. Based on these results, the school officials conclude that a great majority of the parents have no difficulty spending time with their kids after school.

    2. A survey is conducted on a simple random sample of 1,000 women who recently gave birth, asking them about whether they smoked during pregnancy. A follow-up survey asking if the children have respiratory problems is conducted 3 years later. However, only 567 of these women are reached at the same address. The researcher reports that these 567 women are representative of all mothers.

    3. An orthopedist administers a questionnaire to 30 of his patients who do not have any joint problems and finds that 20 of them regularly go running. He concludes that running decreases the risk of joint problems.

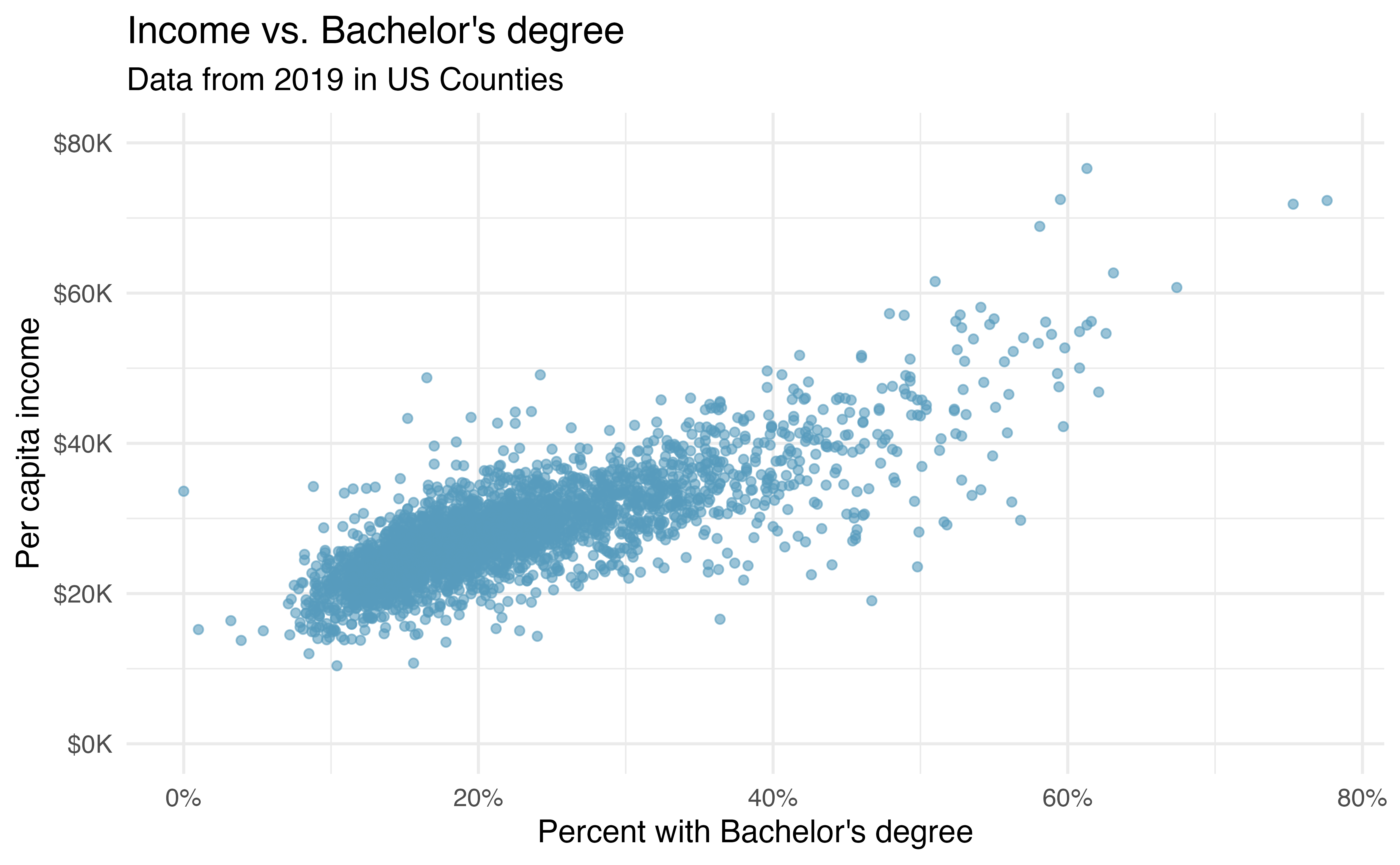
  1. Income and education in US counties. The scatterplot below shows the relationship between per capita income (in thousands of dollars) and percent of population with a bachelor’s degree in 3,142 counties in the US in 2019.13

    1. What are the explanatory and response variables?

    2. Describe the relationship between the two variables. Make sure to discuss unusual observations, if any.

    3. Can we conclude that having a bachelor’s degree increases one’s income?

  1. Eat well, feel better. In a public health study on the effects of consumption of fruits and vegetables on psychological well-being in young adults, participants were randomly assigned to three groups: (1) diet-as-usual, (2) an ecological momentary intervention involving text message reminders to increase their fruits and vegetable consumption plus a voucher to purchase them, or (3) a fruit and vegetable intervention in which participants were given two additional daily servings of fresh fruits and vegetables to consume on top of their normal diet. Participants were asked to take a nightly survey on their smartphones. Participants were student volunteers at the University of Otago, New Zealand. At the end of the 14-day study, only participants in the third group showed improvements to their psychological well-being across the 14-days relative to the other groups. (Conner et al. 2017)

    1. What type of study is this?

    2. Identify the explanatory and response variables.

    3. Comment on whether the results of the study can be generalized to the population.

    4. Comment on whether the results of the study can be used to establish causal relationships.

    5. A newspaper article reporting on the study states, “The results of this study provide proof that giving young adults fresh fruits and vegetables to eat can have psychological benefits, even over a brief period of time.” How would you suggest revising this statement so that it can be supported by the study?

  1. Screens, teens, and psychological well-being. In a study of three nationally representative large-scale datasets from Ireland, the United States, and the United Kingdom (n = 17,247), teenagers between the ages of 12 to 15 were asked to keep a diary of their screen time and answer questions about how they felt or acted. The answers to these questions were then used to compute a psychological well-being score. Additional data were collected and included in the analysis, such as each child’s sex and age, and on the mother’s education, ethnicity, psychological distress, and employment. The study concluded that there is little clear-cut evidence that screen time decreases adolescent well-being. (Orben and Baukney-Przybylski 2018)

    1. What type of study is this?

    2. Identify the explanatory variables.

    3. Identify the response variable.

    4. Comment on whether the results of the study can be generalized to the population, and why.

    5. Comment on whether the results of the study can be used to establish causal relationships.

  1. The question “Over the last five years, what is the average time to complete a degree for Duke undergrads?” is only relevant to students who complete their degree; the average cannot be computed using a student who never finished their degree. Thus, only Duke undergrads who graduated in the last five years represent cases in the population under consideration. Each such student is an individual case. For the question “Does a new drug reduce the number of deaths in patients with severe heart disease?”, a person with severe heart disease represents a case. The population includes all people with severe heart disease.↩︎

  2. Answers will vary. From our own anecdotal experiences, we believe people tend to rant more about products that fell below expectations than rave about those that perform as expected. For this reason, we suspect there is a negative bias in product ratings on sites like Amazon. However, since our experiences may not be representative, we also keep an open mind.↩︎

  3. This is a different concept than a control group, which we discuss in the second principle and in Section 2.2.2.↩︎

  4. Also called a lurking variable, confounding factor, or a confounder.↩︎

  5. Human subjects are often called patients, volunteers, or study participants.↩︎

  6. There are always some researchers involved in the study who do know which patients are receiving which treatment. However, they do not interact with the study’s patients and do not tell the blinded health care professionals who is receiving which treatment.↩︎

  7. The researchers assigned the patients into their treatment groups, so this study was an experiment. However, the patients could distinguish what treatment they received because a stent is a surgical procedure. There is no equivalent surgical placebo, so this study was not blind. The study could not be double-blind since it was not blind.↩︎

  8. Ultimately, can we make patients think they got treated from a surgery? In fact, we can, and some experiments use a sham surgery. In a sham surgery, the patient does undergo surgery, but the patient does not receive the full treatment, though they will still get a placebo effect.↩︎

  9. Answers will vary. Population density may be important. If a county is very dense, then this may require a larger percentage of residents to live in housing units that are in multi-unit structures. Additionally, the high density may contribute to increases in property value, making homeownership unfeasible for many residents.↩︎

  10. Derived from similar figures in Chance and Rossman (2018) and Ramsey and Schafer (2012).↩︎

  11. The data used in this exercise comes from the General Social Survey, 2018.↩︎

  12. The cia_factbook data used in this exercise can be found in the openintro R package.↩︎

  13. The county_complete data used in this exercise can be found in the openintro R package.↩︎